Question

The image of the point $(\alpha ,\beta )$ w.r.t the line $(x + y) = 0$ is
A. $( - \alpha ,\beta )$
B. $(\beta ,\alpha )$
C. $( - \beta , - \alpha )$
D.None of these

Answer 1

Hint : The image of the point is asked with respect to the line. The line will act as a mirror for the point. First, plot the line given and the point. Then use the concept of mirror reflection to see at what point the image of the given point will lie and plot the image with its coordinates.

Complete step-by-step answer :
Given, the point is $P(\alpha ,\beta )$
And the line $(x + y) = 0$
We are asked to find the image of the point $P(\alpha ,\beta )$ w.r.t the line $(x + y) = 0$ that is the line acts as a mirror.
Let us draw the graph for the given line.
The line is
$(x + y) = 0$
$\Rightarrow y = - x$ (i)
The general line equation for straight lines is $y = mx + c$ , where $m$ is the slope of the line and $c$ is the intercept.
Comparing equation (i) with general equation of straight line we get,
Slope of the line as negative and intercept is zero.
Now, we plot the line which acts as a mirror for the given point.

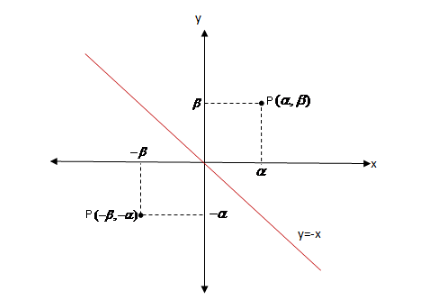
As the line acts as a mirror the image of the point will be its mirror reflection.
Therefore, the image of the point w.r.t the line is $P( - \beta , - \alpha )$ .
So, the correct answer is “Option C”.

Note : In such a type of question where the image of a point is asked with respect to a given line. First try to plot the line, if you observe that the equation of the line given is linear then compare the given line with the general equation of the straight line which is $y = mx + c$ , as we have done for the above equation. And plot the line with the slope and intercept obtained. After that plot the given point and see where its mirror reflection will lie with respect to the line.