Question

The image of P(a, b) on the line y = −x is Q and the image of Q on the line y = x is R. Then the midpoint of PQ is:
a. $\left( {a + b,\;a + b} \right)$ b.$\left( {\dfrac{{a + b}}{2},\dfrac{{b + 2}}{2}} \right)$ c.$\left( {a - b,\;b - a} \right)$ d. (0, 0)

Answer 1

We will first find a general expression for the image of any point about $y = - x$ and $y = x.$ Then we will apply it to P and Q. Once this is done we will use the midpoint formula.

Complete step-by-step answer:

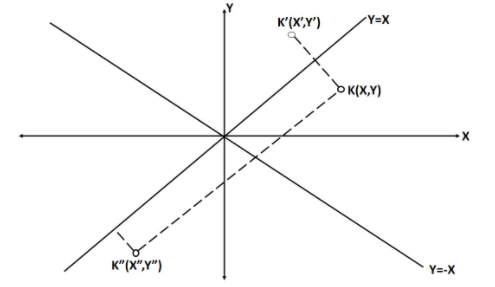
Consider any point K, its reflection about $y = x,$ K’ and its reflection about $y = - x,$ K” .
From the figure it is easy to draw the following conclusions:

K’ has its y and x interchanged from k, that is, K’(x’, y’) = K (y, x)
K” is analogous to K’ but has negative coordinate that is, K”(x”, y”) = K’(−x’, −y’) = K(−y, −x)

Using this, we can say that:
Coordinates of ${\text{Q}} = \left( { - b, - a} \right)$ (reflect P along $y = - x$)
Coordinates of ${\text{R}} = \left( { - a, - b} \right)$ (reflect Q along $y = - x$)
Coordinates interchange.

Now, the midpoint formula can be applied on P and R.
Let the midpoint be T.

x coordinate of ${\text{T}} = \dfrac{{{x_p} + {x_R}}}{2} = \dfrac{{a - a}}{2} = 0$
y coordinate of $T = \dfrac{{{y_p} + {y_R}}}{2} = \dfrac{{b - b}}{2} = 0$

Hence the midpoint is $\boxed{0,0.}$.
Option D is correct.

Note: Follow the following method to get the reflection of any point P(x,y) about line L: ax + by + c = 0.
1.Write the equation of a line with the slope perpendicular to L, ie,
N: bx - ay + d = 0.
2.Find out the value of d by substituting the value of P(x, y) in the equation.
3.Write the general coordinates of point Q(x’, y’) in terms of the equation N, ie, the coordinates would be (x’, (bx’-d)/a)
4.Now apply the condition that the perpendicular distance of Q from line L is equal to the perpendicular distance of P from line L. You can find the perpendicular distance of point P from L by the following formula :
$(ax + by + c)/\sqrt{(a^2 + b^2)}$, where x and y are the coordinates of P.
5.Find the value of x’ that satisfies the above condition.
6.Substitute the value of x’ in the coordinates in step 3 to find x’, y’ of the reflected point Q.