Question

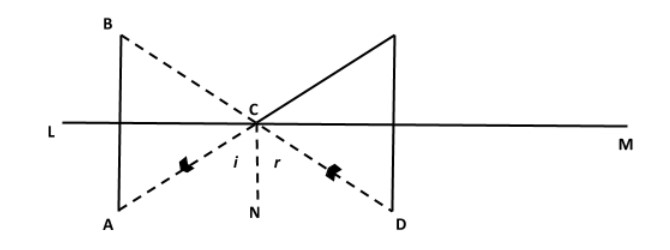
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in Fig. Prove that the image is as far behind the mirror as the object is in front of the mirror.

Answer 1

Hint: A plane mirror is a mirror with a flat surface. For light rays striking a plane mirror the angle of incidence, (angle between the incident ray and the normal) and the angle of reflection (angle between reflected ray and normal) are equal. Here, in the question the object is placed before a plane mirror LM, whose image is seen at B by an observer at D.
Given: The image of an object is placed at a point A before a plane mirror LM is seen at point B by an observer at D. Here, we need to prove that the image is as far behind the mirror as the object in front of the mirror.

Complete step-by-step answer :
Prior to solving the question we mark the point of intersection of the line AB and the mirror LM to be T.

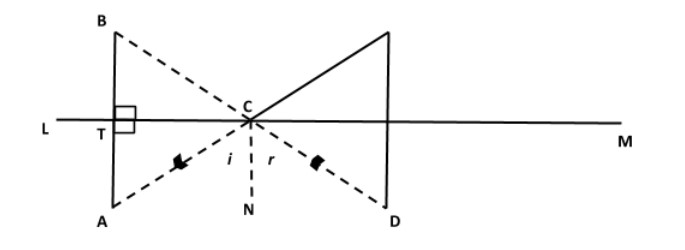
So, according to the figure, we need to prove that
$AT = BT$
We know that,
Angle of incidence = Angle of reflection
So, we get,
$\angle ACN = \angle DCN \to \left( 1 \right)$
We know that,
$AB\parallel CN$ and AC is the transversal
Therefore,
$\angle TAC = \angle ACN \to \left( 2 \right)$ [Alternate Angle]
Again,
$AB\parallel CN$ and BD is the transversal
From the figure, we know that and are corresponding angles
$\angle TBC = \angle DCN \to \left( 3 \right)$
By considering the equation (1), (2) and (3)
We get,
$\angle TBC = \angle TAC \to \left( 4 \right)$
Now, in and
$\angle ATC = \angle BTC = 90^\circ$
Is common, that is $CT = CT$
$\angle TBC = \angle TAC$ [From equation (4)]
By AAS congruence criteria,

 $\therefore AT = BT$ (Corresponding Parts of Congruent Triangles)  

Therefore, it is proved that the image is as far behind as the object is in front.

Note: Some students may find it confusing about AB being perpendicular to LM. But in the case of plane mirrors, a straight line joining object point and image point is always perpendicular to the mirror.