Question

The image of an ellipse $4{x^2} + 9{y^2} = 36$ in the line $x + y - 1 = 0$ is
A) $\dfrac{{{{\left( {x + 1} \right)}^2}}}{4} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{9} = 1$
B) $\dfrac{{{{\left( {x - 1} \right)}^2}}}{9} + \dfrac{{{{\left( {y - 1} \right)}^2}}}{4} = 1$
C) $\dfrac{{{{\left( {x - 1} \right)}^2}}}{4} + \dfrac{{{{\left( {y - 1} \right)}^2}}}{9} = 1$
D) $\dfrac{{{{\left( {x + 1} \right)}^2}}}{9} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{4} = 1$

Answer 1

Here we will firstly convert the given equation of ellipse into the general equation of ellipse. Then we will assume the coordinates of the mirror image of the center of the ellipse on the given line. From this we will get the equation of the image of the ellipse. We will then find the coordinates of the mirror image of the center of the ellipse on the line by using the basic concept of lines. Further we will put the coordinates in the equation of the image of the ellipse.

Complete step by step solution:
First, we will convert the equation $4{x^2} + 9{y^2} = 36$ into the general form of the ellipse. So, we get
$\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1$
It is given that the image of the ellipse is in the line $x + y - 1 = 0$. Let $\left( {h,k} \right)$ be the coordinates of the mirror image of the center of the ellipse on the line.
Therefore, the equation of the image of the ellipse will be,
$\dfrac{{{{\left( {x - h} \right)}^2}}}{4} + \dfrac{{{{\left( {y - k} \right)}^2}}}{9} = 1$…………………$\left( 1 \right)$

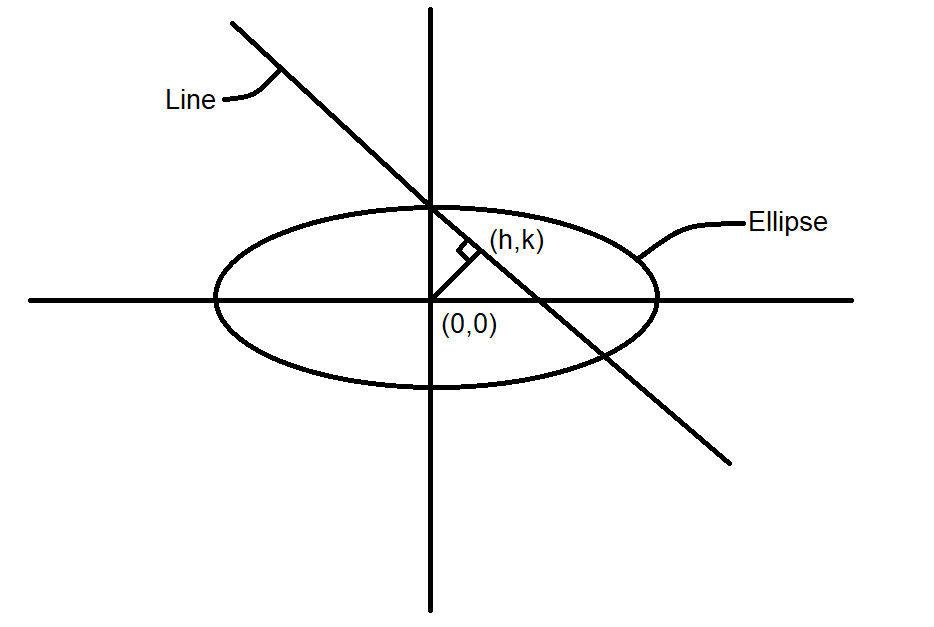
Now we know that the midpoint of both the centers i.e. $\left( {0,0} \right)$ and $\left( {h,k} \right)$ lies on the line $x + y - 1 = 0$and the coordinates of the midpoint of the centers is $\left( {\dfrac{{h + 0}}{2},\dfrac{{k + 0}}{2}} \right) = \left( {\dfrac{h}{2},\dfrac{k}{2}} \right)$. So, this coordinate must satisfy the line equation. Therefore, we get
$\Rightarrow \dfrac{h}{2} + \dfrac{k}{2} - 1 = 0$
$\Rightarrow \dfrac{h}{2} + \dfrac{k}{2} = 1$
On taking LCM and cross multiplying the terms, we get
$\Rightarrow h + k = 2$…………………$\left( 2 \right)$
We know that the line joining the centers is perpendicular to the given line. Therefore, we get
$\Rightarrow \dfrac{{k - 0}}{{h - 0}} = 1$
Simplifying the expression, we get
$\Rightarrow k = h$…………………$\left( 3 \right)$
So, from the equation $\left( 2 \right)$ and equation $\left( 3 \right)$ we get
$\Rightarrow h + h = 2$
$\Rightarrow 2h = 2$
Dividing both sides by 2, we get
$\Rightarrow h = 1$
$\Rightarrow h = k = 1$
Now we get the value of the point $\left( {h,k} \right)$ as $\left( {1,1} \right)$. So, we will put this value in the equation of the image of the ellipse i.e. equation $\left( 1 \right)$. So, we get
$\dfrac{{{{\left( {x - 1} \right)}^2}}}{4} + \dfrac{{{{\left( {y - 1} \right)}^2}}}{9} = 1$

Hence, option C is the correct option.

Note:
Here we have to keep in mind that in case of an ellipse the sum of the focal distances of any point on an ellipse is equal to its major axis. Ellipse is an oval type shape which has a minor and major axis.
The basic equation of the ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, where $a$ is the distance of the end of major axis from the center and $b$ is the distance of the end of minor axis from the center.
We need to keep in mind that If any curve or line passes through a point then the value of the coordinate of the point always satisfies the equation of the curve.