Question

The hypotenuse of a right angled triangle is 41 cm and the area of the triangle is 180 sq. cm, then the difference between the lengths of the legs of the triangles must be?
(a) 22 cm
(b) 25 cm
(c) 31 cm
(d) 27 cm

Answer 1

Hint: Draw a right angle triangle right angled at B and assume the sides as ‘a’ and ‘c’ lying opposite to that of angles A and C respectively. Now, use the formula of area of a triangle given by: Area = $\dfrac{1}{2}\times \text{base}\times \text{height}$, where ‘a’ can be substitutes as base and ‘c’ as height. Assume this expression as equation (i). Now apply Pythagoras theorem given as: $\text{hypotenus}{{\text{e}}^{2}}=\text{perpendicula}{{\text{r}}^{2}}+\text{bas}{{\text{e}}^{2}}$ to form another equation (ii). Subtract equation (i) from equation (ii) and use the formula: ${{a}^{2}}+{{c}^{2}}-2ac={{\left( a-c \right)}^{2}}$ to simplify the term. Take the square root on both sides to get the answer.

Complete step-by-step answer:
__
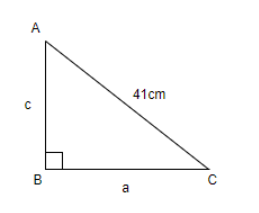
Let us assume a right angle triangle right angled at B and assume the sides as ‘a’ and ‘c’ lying opposite to that of angles A and C respectively. Considering ‘a’ as base and ‘c’ as height, we have,
$\text{Area}=\dfrac{1}{2}\times \text{base}\times \text{height}$
Substituting all the values provided, we have,
$\begin{aligned} & 180=\dfrac{1}{2}\times a\times c \\\ & \Rightarrow ac=360 \\\ & \Rightarrow 2ac=720...............(i) \\\ \end{aligned}$
Now applying Pythagoras theorem, we have,
$\begin{aligned} & \text{hypotenus}{{\text{e}}^{2}}=\text{perpendicula}{{\text{r}}^{2}}+\text{bas}{{\text{e}}^{2}} \\\ & \Rightarrow {{41}^{2}}={{a}^{2}}+{{c}^{2}} \\\ & \Rightarrow {{a}^{2}}+{{c}^{2}}={{41}^{2}}.................(ii) \\\ \end{aligned}$
Subtracting equation (i) from equation (ii), we get,
$\begin{aligned} & {{a}^{2}}+{{c}^{2}}-2ac={{41}^{2}}-720 \\\ & \Rightarrow {{\left( a-c \right)}^{2}}=1681-720 \\\ & \Rightarrow {{\left( a-c \right)}^{2}}=961 \\\ \end{aligned}$
Taking square root on both sides, we have,
$\begin{aligned} & \left( a-c \right)=\sqrt{961} \\\ & \Rightarrow \left( a-c \right)=31 \\\ \end{aligned}$
Hence, option (c) is the correct answer.

Hint: One may note that we do not have to add the two equations because we have to find the difference of two legs and not the sum. If we will add the two equations then also we can get the answer but that would be repeating the same process, so it will be a lengthy process. One important thing to note is that we must not apply Herons’ formula to determine the area of the triangle. If we will do so then we have to counter some difficult calculations.