Question

The horizontal distance between two towers is $60m$ and the angle of depression of the top of the first tower as seen from the top of the second is ${30^ \circ }$. If the height of the second tower is $90m$ then the height of the first tower is
A. $90m$
B. $(150 - 60\sqrt 3 )m$
C. $(150 - 20\sqrt 3 )m$
D. None of these

Answer 1

Hint : It is given that the angle of the depression is seen from the second tower which concludes that the height of the second is more than that of the first tower . Always draw a figure with given data. We have made use of trigonometric ratios to find out the height of the first tower. Different ratios have different values like perpendicular , base hypotenuse .

Complete step-by-step answer :
For better understanding we have to draw a figure with given measurements .

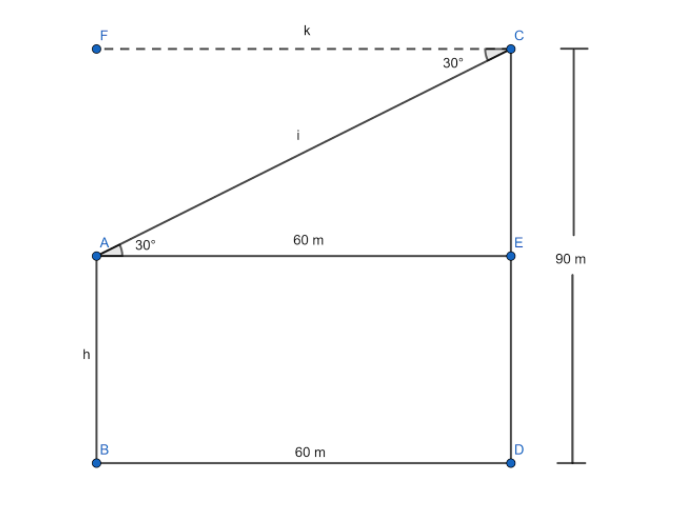
Here $A$ is the point at the top of the first tower . C is the point of top of the second tower with an angle of depression of ${30^ \circ }$towards the top of the first tower . Now the $\angle CAE = {30^ \circ }$ ( by alternate interior angle property ) . Now in $\vartriangle CAE$ we have
$\tan {30^ \circ } = \dfrac{{CE}}{{AE}}$ , now $CE = CD - ED$ , which is $CE = 90 - h$
Therefore , $\tan {30^ \circ } = \dfrac{{90 - h}}{{60}}$ ,
now as we know the value of $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ we get ,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{90 - h}}{{60}}$
On solving we get
$\dfrac{{60}}{{\sqrt 3 }} = 90 - h$ ,
on rationalizing the RHS we get ,
$\dfrac{{60\sqrt 3 }}{3} = 90 - h$ ,
on solving we get
$90 - h = 20\sqrt 3$
On simplifying we get
$h = 90 - 20\sqrt 3$ ,
putting the value of $\sqrt 3$ as $\sqrt 3 = 1.732$ we get ,
$h = 90 - 20 \times 1.732$
On solving we get
$h = 90 - 34.64$ ,
on solving we get
$h = 55.36m$
Which is the height of the first tower and the required answer . Therefore , option (4) is the correct answer .
So, the correct answer is “Option 4”.

Note: These questions related to angle of depression and angle of elevation are related to applications of the trigonometric identities which are also applied practically . Trigonometry is widely used in navigation and geography to locate different places in relation to the latitude and longitude .