Question

The horizontal distance between two towers is $140m.$ The angle of elevation of the top of the first tower, when seen from the top of the second tower is $30^\circ$ . If the height of the second tower is $60m.$ find the height of the first tower.

Answer 1

Hint : First of all we will draw the diagram using the given data, the angle here used is the angle of elevation to observe the top of the other tower and then finding the correlation between the known and the unknown terms will find the height of the first tower.

Complete step-by-step answer :

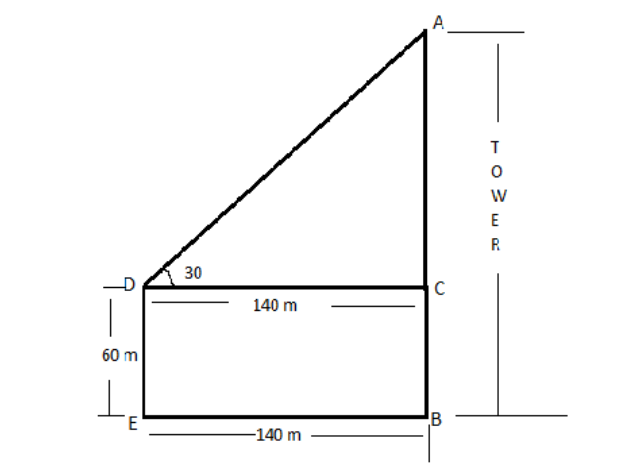
In the above figure, we can observe that AB is the tower with the height “h” and the other tower is ED with height $= 60m$
Distance between both the towers is,
$EB = DC = 140m$
Given that angle of elevation is $\angle ADC = 30^\circ$
$\Delta ACD$ forms the right angled triangle, tangent can be expressed as the opposite side upon the adjacent side.
$\tan 30^\circ = \dfrac{{AC}}{{DC}}$
By referring to the trigonometric table and the given data place the values in the above expression.
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{h - 60}}{{140}}$
Cross multiply in the above expression, when the denominator is multiplied with the numerator of the opposite side and vice-versa.
$h - 60 = \dfrac{{140}}{{\sqrt 3 }}$
Make the required term the subject,
$h = \dfrac{{140}}{{\sqrt 3 }} + 60$
Simplify the above expression –
$h = 140.8m$
Therefore, the height of the first tower is $140.8\;m$
So, the correct answer is “ $140.8\;m$ ”.

Note : In these types of height and distance problems, we need to first draw the correct figure then place the values (dimensions) given in the problem correctly. We need to be very keen to choose the correct trigonometric ratio and its relation with proper angle. The assign values against angles and segments and solve.