Question

The horizontal component of the Earth's magnetic field at a certain place is $3 \times {10^{ - 5}}T$ and the direction of the field is from the geographic south to the geographic north. A very long straight conductor is carrying a steady current of $1A$ . The force per unit length on it, when it is placed on a horizontal table and the direction of the current is east to west is :
A. $3 \times {10^{ - 5}}N{m^{ - 1}}$
B. $6 \times {10^{ - 3}}N{m^{ - 1}}$
C. $9 \times {10^{ - 2}}N{m^{ - 1}}$
D. $12 \times {10^{ - 6}}N{m^{ - 1}}$

Answer 1

When the current carrying conductor is placed on a horizontal table, only the horizontal component of the earth’s magnetic field will exert a force on it. Applying the basic formula for force exerted by a magnetic field on a current carrying conductor and then dividing the resultant equation by the total length of the conductor, we get the answer.

Formulae used:
$F = liB\sin \theta$ where $F$ is the force exerted by the magnetic field on the current carrying conductor, $l$ is the length of the current carrying conductor, $i$ is the amount of current present in the current carrying conductor, $B$ is the magnetic field and $\theta$ is the angle between the magnetic field and the current carrying conductor.

Complete step by step answer:
According to the given question
Horizontal component of earth’s magnetic field ${B_x} = 3 \times {10^{ - 5}}T$
Current carried by the conducting wire $i = 1A$

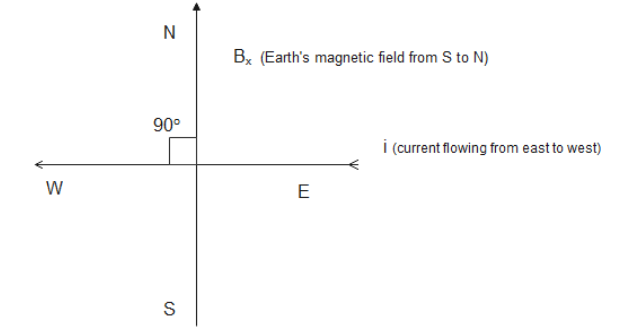
From the equation which gives the value of the force exerted by a magnetic field on a current carrying conductor, we have
$F = li{B_x}\sin \theta$ (where $F$ is the force exerted by the magnetic field on the current carrying conductor, $l$ is the length of the current carrying conductor, $i$ is the amount of current present in the current carrying conductor, ${B_x}$ is the horizontal component of earth’s magnetic field and $\theta$ is the angle between the magnetic field and the current carrying conductor)

From the above diagram, we can clearly see that angle $\theta = 90^\circ$. Thereafter, the equation becomes
$\Rightarrow F = li{B_x}\sin 90^\circ$
$\Rightarrow F = li{B_x}$ ( Since $\sin 90^\circ = 1$ )
Now, for finding the force per unit length, we divide the equation by total length of the current carrying wire $l$
\Rightarrow \dfrac{F}{l} = \dfrac{{li{B_x}}}{l} \\\
$\Rightarrow f = i{B_x}$
where $f$ is force per unit length.
Substituting the respective values, we get
$\Rightarrow f = 1 \times 3 \times {10^{ - 5}}N{m^{ - 1}} \\\ \therefore f = 3 \times {10^{ - 5}}N{m^{ - 1}} \\\$
Thus, the correct answer to the question is option A.

Note: The equation $F = liB\sin \theta$ comes from the equation $\overrightarrow F = l\overrightarrow i \times \overrightarrow B$ . Since the equation involves a cross product of two vectors, the equation becomes $F = liB\sin \theta$ . Here, $\theta$ is actually the angle between the current and the magnetic field. To determine $\theta$ , we use the directions of the fields and the directions of the current given to us.