Question

The horizontal beam in figure weights $150N$, and its centre of gravity is at its centre. Find the horizontal and the vertical component of the forces exerted on the beam at the wall.

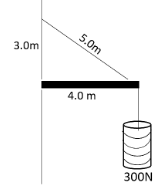
A. horizontal component is $500N$ towards left and vertical component $75N$ downwards.
B. horizontal component is $500N$ towards right and vertical component $75N$ .
C. horizontal component is $625N$ towards left and vertical component $150N$.
D. Horizontal component is $625N$ towards right and vertical component $150N$ downwards.

Answer 1

Torque is the quantity of the force that can cause an object to rotate about an axis. Force is what makes an object to accelerate in linear kinematics. In the same way, torque is what causes an angular acceleration. Hence, torque can be described as the rotational equivalent of linear force.

Complete answer:
Here the resultant torque on the beam about the hinge becomes zero.

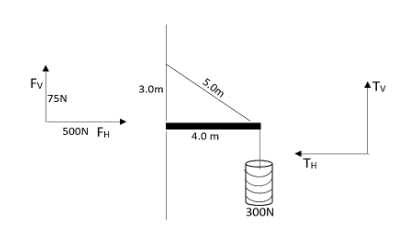
Let the horizontal component & vertical component of tension be ${{T}_{H}},{{T}_{V}}$ respectively. And the horizontal component & vertical component of forces exerted on the beam at the wall are ${{F}_{H}},{{F}_{V}}$ respectively. Therefore we can write that,

$\begin{aligned} & {{T}_{V}}\times 4-300\times 4-150\times 2=0 \\\ & {{T}_{V}}=375N \\\ \end{aligned}$

This tension will be acting upwards.
By geometry, the relation between ${{T}_{H}},{{T}_{V}}$ will be,
$\dfrac{{{T}_{V}}}{{{T}_{H}}}=\dfrac{3}{4}$
Hence we will get,
${{T}_{H}}=400N$
This is acting on the left side.
Now let us balance the force,
${{T}_{H}}+{{F}_{H}}=0$
Therefore
${{F}_{H}}=500N$
This is acting on the right side.
And also we can write that,
${{F}_{V}}+{{T}_{V}}-300-150=0$
${{F}_{V}}=450-375=75N$
This is acting upwards.

So, the correct answer is “Option B”.

Note:
The centre of gravity is the average location on the basis of the weight of an object. We can completely define the motion of any object through space in terms of the movement of the centre of gravity of the object from one place to another, and the rotation of the object about its centre of gravity when it is free to rotate.