Question
Question: The height of water in a vessel is \( h \) . The vessel wall of width \( b \) is at an angle \( \the...
The height of water in a vessel is h . The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is:
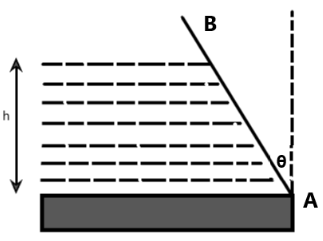
(A) 21ρbh2gcosθ
(B) 21ρbh2g
(C) 21ρbh2gsecθ
(D) Zero
Solution
Hint : The length of the wall in contact with the water when it is bent is longer than the length if it had not been at angle to the vertical. So we can find the force from the formula, F=PA where we have to substitute the average pressure and the area will be the area that is in contact with the fluid.
Formula used: In this solution we will be using the following formula;
F=PA where P is the pressure on a surface, F is the force exerted on that surface, and A is the area of the surface.
P=ρgh where P is the pressure at a particular point in a fluid, ρ is the density of the fluid, and g is acceleration due to gravity, and h is the depth from the free surface of the liquid.
Complete step by step answer:
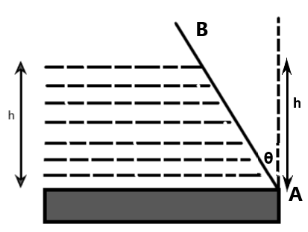
Observe that the length of the wall in contact with the water is higher at an angle to the vertical than if it were exactly vertical. From diagram, we see that
h=lcosθ
hence,
l=cosθh=hsecθ
Now, the pressure of liquid at a particular depth below the surface is given as
P=ρgh where P is the pressure at a particular point in a fluid, ρ is the density of the fluid, and g is acceleration due to gravity, and h is the depth from the free surface of the liquid.
However, in such a vessel, the average pressure act at 2h of the vessel, hence the average pressure on the surface is given as
Pave=ρg2h
Hence, the net force is
Fave=FNET=PaveA
The area in contact with the fluid is given as
A=lb where l is the total length, and b is the width.
But l=hsecθ hence,
A=bhsecθ
Then Fave=ρg2hbhsecθ
⇒Fave=21ρbh2gsecθ
Hence, the correct option is C.
Note:
For clarity, the position of the average pressure can be proven from
Pave=A1∫0hPdA=A1∫0hρghdA as follows
In this case,
dA=bdl since width is the same and we are gradually moving up along the length.
But l=hsecθ
⇒dl=dhsecθ
Hence,
By inserting dA=bdhsecθ into A1∫0hρghdA we have
Pave=bhsecθ1∫0hρghbdhsecθ
⇒Pave=bhsecθ1ρg2h2bsecθ
Then, by cancelations,
Pave=ρg2h
Which implies that the average pressure acts at depth or height 2h (exactly at the middle of the vessel).
