Question

The height of the chimney in (m) when it is found that on walking towards it $\;{\text{50m}}$ in the horizontal line through its base, the angle of elevation of its top changes from ${30^ \circ }$ to ${60^ \circ }$ is
A. ${\text{25}}$
B. ${\text{25}}\sqrt 2$
C. ${\text{25}}\sqrt 3$
D.None of these

Answer 1

Hint : We are asked to find the height of the chimney. First draw a diagram according to the conditions given in the question for both angles of elevation. Then use the trigonometric identities for the triangles formed to find the height of the chimney.

Complete step-by-step answer :
Given, distance walked on the horizontal line $d = 50\;{\text{m}}$
Angle of elevation changes from ${30^ \circ }$ to ${60^ \circ }$
Let us draw a diagram

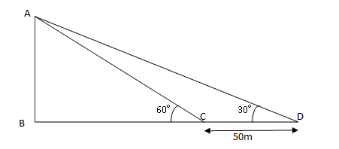
Here, AB is the height of the chimney and CD is the distance moved towards the chimney.
We observe that triangles ABC and ABD are right angled triangles.
In triangle ABC, using trigonometric identity of
${\text{tan}}\theta {\text{ = }}\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$ for angle $\angle BCA$ we have,

\Rightarrow BC = \dfrac{{AB}}{{\tan {{60}^ \circ }}} $$ $$ \Rightarrow BC = AB\cot {60^ \circ }$$ (i) Similarly, in triangle ABD using trigonometric identity of $${\text{tan}}\theta {\text{ = }}\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$$ for angle $$\angle BDA$$ we have, $$\tan {30^ \circ } = \dfrac{{AB}}{{BD}} \\\ \Rightarrow BD = \dfrac{{AB}}{{\tan {{30}^ \circ }}} $$ $$ \Rightarrow BD = AB\cot {30^ \circ }$$ (ii) We have from the diagram, $$CD = BD - BC$$ Putting the values of BD and BC from equations (i) and (ii), we get $$CD = AB\cot {30^ \circ } - AB\cot {60^ \circ }$$ Now, putting the value of CD we get, $$50 = AB\cot {30^ \circ } - AB\cot {60^ \circ } \\\ \Rightarrow AB(\cot {30^ \circ } - \cot {60^ \circ }) = 50 \\\ \Rightarrow AB\left( {\sqrt 3 - \dfrac{1}{{\sqrt 3 }}} \right) = 50 $$ $$ \Rightarrow AB = \dfrac{{50\sqrt 3 }}{{3 - 1}} = \dfrac{{50\sqrt 3 }}{2} = 25\sqrt 3\; {\text{m}}$$ Therefore, the height of the chimney is $$25\sqrt 3\; {\text{m}}$$ . **So, the correct answer is “Option C”.** **Note** : Angle of elevation is the angle between the horizontal line and line of sight. Here, line of sight can be said as an imaginary line drawn from the boy’s eyes to the top of the tower. Whenever such questions are given, use the trigonometric identities for sine, cosine and tangent to find the height of an object or distance between the object and the body.