Question
Question: The height of mercury column measured with brass scale at temperature $t_1$ is $n_1$ units. Height o...
The height of mercury column measured with brass scale at temperature t1 is n1 units. Height of the mercury column measured by brass scale at t = 0∘C is n2 units. The coefficient of linear expansion of brass is α and coefficient of volume expansion of mercury is γ. (Assume the expansion in area of vessel containing mercury is negligible).
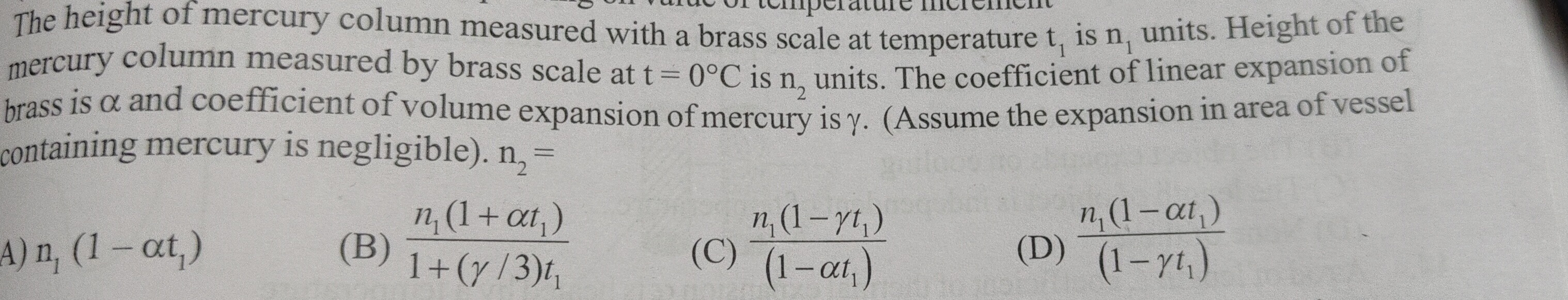
n_1 (1 - \alpha t_1)
1+(γ/3)t1n1(1+αt1)
(1−αt1)n1(1−γt1)
(1−γt1)n1(1−αt1)
1+γt1n1(1+αt1)
Solution
Let htrue(T) be the true height of the mercury column at temperature T. Let Lscale(T) be the length of one unit on the brass scale at temperature T. Let Lscale(0) be the length of one unit on the brass scale at 0∘C. Then, Lscale(t1)=Lscale(0)(1+αt1).
At temperature t1, the reading on the scale is n1. This means the true height of the mercury column is: htrue(t1)=n1×Lscale(t1)=n1×Lscale(0)(1+αt1).
At temperature 0∘C, the reading on the scale is n2. This means the true height of the mercury column is: htrue(0)=n2×Lscale(0).
The true height of the mercury column itself expands with temperature. Thus, the true height at t1 is related to the true height at 0∘C by: htrue(t1)=htrue(0)(1+γt1).
Substituting the expressions for htrue(t1) and htrue(0): n1×Lscale(0)(1+αt1)=[n2×Lscale(0)](1+γt1).
Canceling Lscale(0) from both sides: n1(1+αt1)=n2(1+γt1).
We need to find n2. Rearranging the equation: n2=1+γt1n1(1+αt1).
Comparing this result with the given options, none of the options exactly match. However, if we assume there might be a typo in the options and consider the structure of similar problems, the derived answer is 1+γt1n1(1+αt1). Given the provided options, it's highly probable that there is an error in the question or its options. The correct answer is 1+γt1n1(1+αt1).
