Solveeit Logo
Login

Question

Question: The height of a tower is h and the angle of elevation of the top of the tower is \(\alpha \) on movi...

The height of a tower is h and the angle of elevation of the top of the tower is α\alpha on moving a distance h/2 towards the tower, the angle of elevation becomes β\beta . What is the value of cot⁡α−cot⁡β\cot \alpha - \cot \beta .

Explanation

Solution

In this particular question first draw the pictorial representation of the give problem it will give us a clear picture of what we have to find out later in the solution use the concept that (tan x = perpendicular/base) in a right triangle and tan x = (1/cot x), so use these concepts to reach the solution of the question.

Complete step-by-step answer:

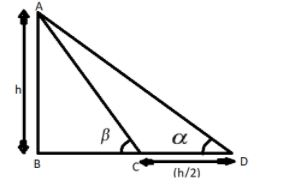
Let us consider the tower AB as shown in the figure, it is given that the height of the tower is h.
So AB = h (as shown in the figure).
Now the angle of elevation of the top of the tower is α\alpha as shown in the figure.
Now it is given when we move towards the tower i.e. from point D to point C as shown in the figure the angle of elevation changes to β\beta and the distance DC is (h/2).
Now we have to find out the value of cot⁡α−cot⁡β\cot \alpha - \cot \beta .
Now in triangle ABC,
Tan is tan of the angle is the ratio of perpendicular to base.
Therefore, tan⁡β=ABBC\tan \beta = \dfrac{{AB}}{{BC}}
Now substitute the value of AB we have,
⇒tan⁡β=hBC\Rightarrow \tan \beta = \dfrac{h}{{BC}}
Now as we know that tan x = 1/cot x, so use this property in the above equation we have.
⇒cot⁡β=BCh\Rightarrow \cot \beta = \dfrac{{BC}}{h}
⇒hcot⁡β=BC\Rightarrow h\cot \beta = BC.................. (1)
Now in triangle ABD we have,
⇒tan⁡α=ABBD\Rightarrow \tan \alpha = \dfrac{{AB}}{{BD}}
Now, BD = BC + CD
Therefore,
⇒tan⁡α=ABBC+CD\Rightarrow \tan \alpha = \dfrac{{AB}}{{BC + CD}}
Now substitute the value of, AB, BC and CD we have,
⇒tan⁡α=hhcot⁡β+h2\Rightarrow \tan \alpha = \dfrac{h}{{h\cot \beta + \dfrac{h}{2}}}
Now simplify i.e. cancel out h from numerator and denominator we have,
⇒tan⁡α=1cot⁡β+12\Rightarrow \tan \alpha = \dfrac{1}{{\cot \beta + \dfrac{1}{2}}}
⇒cot⁡α=cot⁡β+121\Rightarrow \cot \alpha = \dfrac{{\cot \beta + \dfrac{1}{2}}}{1}
⇒cot⁡α=cot⁡β+12\Rightarrow \cot \alpha = \cot \beta + \dfrac{1}{2}
⇒cot⁡α−cot⁡β=12\Rightarrow \cot \alpha - \cot \beta = \dfrac{1}{2}
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that in trigonometry sin x = perpendicular to hypotenuse, cos x = base to hypotenuse and tan x = perpendicular to base and always remember that sin x = (1/cosec x), cos x = (1/sec x) and tan x = (1/cot x).