Solveeit Logo
Login

Question

Question: The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. I...

The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If the volume of the small cone is 127\dfrac{1}{27} that of the given cone, at what height above the base is the section made?

Explanation

Solution

Hint:First we will draw the figure of a cone and then using all the values that are given in the question we will find the volume of the cone. After we know that the volume of the smaller cone will be 127\dfrac{1}{27} of the larger cone and by using this much information we will find the height of the smaller cone.

Complete step-by-step answer:

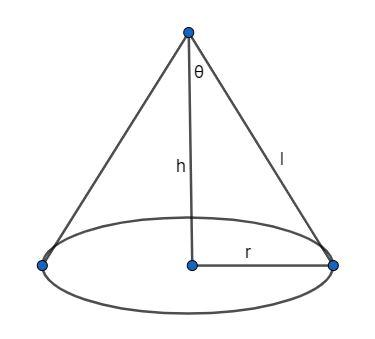
The value of h = 30 cm and r = radius of base.
Let θ\theta be the angle between height (h) and slant height (l) in the above figure.
The formula for volume of cone is πr2h3\dfrac{\pi {{r}^{2}}h}{3} .
A right angle triangle is formed where base = radius, height = h and hypotenuse = slant height.
As we know tan⁡θ=baseheight\tan \theta =\dfrac{base}{height} .
From above we get tan⁡θ=rh\tan \theta =\dfrac{r}{h} ⇒r=htan⁡θ\Rightarrow r=h\tan \theta ………….. (1)
After cutting the cone, let the height of the smaller cone be h’ and radius be r’.
The relation between h’ and r’ is r′=h′tan⁡θr'=h'\tan \theta …………….. (2)
Now the volume of larger cone using equation (1) is πr2h3\dfrac{\pi {{r}^{2}}h}{3}=πh3tan⁡2θ3\dfrac{\pi {{h}^{3}}{{\tan }^{2}}\theta }{3} …………. (3)
Now the volume of smaller cone using equation (2) is πr′2h′3=πh′3tan⁡2θ3\dfrac{\pi r{{'}^{2}}h'}{3}=\dfrac{\pi h{{'}^{3}}{{\tan }^{2}}\theta }{3}………….. (4)
We know that the volume of a smaller cone will be 127\dfrac{1}{27} of the larger cone.
So, equation(4)equation(3)=127\dfrac{equation(4)}{equation(3)}=\dfrac{1}{27}
⇒πh′3tan⁡2θ3πh3tan⁡2θ3 ⇒h′3h3=127  ⇒h′3=h327 ⇒h′=h3=303=10 \begin{aligned} & \Rightarrow \dfrac{\dfrac{\pi h{{'}^{3}}{{\tan }^{2}}\theta }{3}}{\dfrac{\pi {{h}^{3}}{{\tan }^{2}}\theta }{3}} \\\ & \Rightarrow \dfrac{h{{'}^{3}}}{{{h}^{3}}}=\dfrac{1}{27} \\\ & \\\ & \Rightarrow h{{'}^{3}}=\dfrac{{{h}^{3}}}{27} \\\ & \Rightarrow h'=\dfrac{h}{3}=\dfrac{30}{3}=10 \\\ \end{aligned}
Therefore, h’ = 10 cm.

Note: In this question the important part is to understand how we substituted the radius in terms of height with the use of angle because in both smaller and larger cones the angle θ\theta is the same hence, we used this fact to convert our volume equation containing the only variable height.Students should not get confuse with slant height and height of the cone as they are both different as shown in the figure.