Question

The greatest positive argument of a complex number satisfying $\left| {z - 4} \right| = \operatorname{Re} (z)$ is
A. $\dfrac{\pi }{3}$
B. $\dfrac{{2\pi }}{3}$
C. $\dfrac{\pi }{2}$
D. $\dfrac{\pi }{4}$

Answer 1

Knowing the basic concept that let the complex number be $z = x + iy$. Substitute it in the above equation and take modulus as $z = \sqrt {{x^2} + {y^2}}$and hence equate it with the real part of $z$. Hence, the argument of a complex number can be given as $\arg .z = \tan \dfrac{y}{x}$. Hence, substituting above values the required work can be done.

Complete step by step answer:

The given equation is $\left| {z - 4} \right| = \operatorname{Re} (z)$ and so substitute the value of $z = x + iy$in above equation as
$\left| {x + iy - 4} \right| = \operatorname{Re} (x + iy)$
Hence, on simplifying
\Rightarrow $$$$\left| {x - 4 + iy} \right| = x
Now take the modulus of L.H.S as,
\Rightarrow $$$$\sqrt {{{\left( {x - 4} \right)}^2} + {y^2}} = x
On squaring both side
\Rightarrow $$$${\left( {\sqrt {{{\left( {x - 4} \right)}^2} + {y^2}} } \right)^2} = {x^2}
On simplifying the terms inside the bracket also and so,
\Rightarrow $$$${x^2} - 8x + 16 + {y^2} = {x^2}
On simplification,
\Rightarrow $$$${y^2} = 8(x - 2)
Hence, the given equation is of parabola
Compare it with the general equation and so the focus of parabola be $\left( {4,0} \right)$.
Hence, the parabola drawn can have two possible tangents at a right angle to each other as,
Diagram:

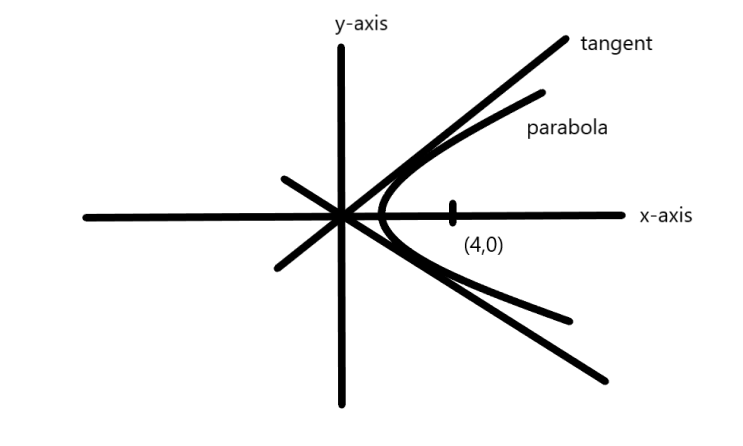
Hence, the pair of the tangent from the directrix is at the right angle and so for a complex number, the possible highest argument can be
given as $\dfrac{\pi }{4}$.
Hence, option(D) is the correct answer.

Note: A complex number is a number that can be expressed in the form $a + ib$, where a and b are real numbers, and i represents the imaginary unit, satisfying the equation ${i^2} =- 1$. Because no real number satisfies this equation, i is called an imaginary number.