Question

The gravitational force exerted by the Sun on the Moon is about twice as great as the gravitational force exerted by the earth on the moon, but still the Moon is not escaping from the gravitational influence of the earth. Mark the option which correctly explains the above system.
A. Escape speed is independent of the direction in which it is projected.
B. The rotational effect of the earth plays a role in the computation of escape speed, however small it may be.
C. A body thrown in the eastward direction has less escape speed.
D. None of the above.

Answer 1

For the moon to be able to escape the gravitational influence of earth, the gravitational pull in between the Sun and the Moon must escape the gravitational influence of the Earth. The gravitational force in between two bodies is given by, $F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}={{m}_{2}}g$, where ${{m}_{2}}$in this case will be the moon and g, the acceleration due to gravity due to the body ${{m}_{1}}$.

Complete step-by-step solution:
Let’s see what information does the gravitational force formula for the Sun-Moon system and the Earth-Moon system provide us.

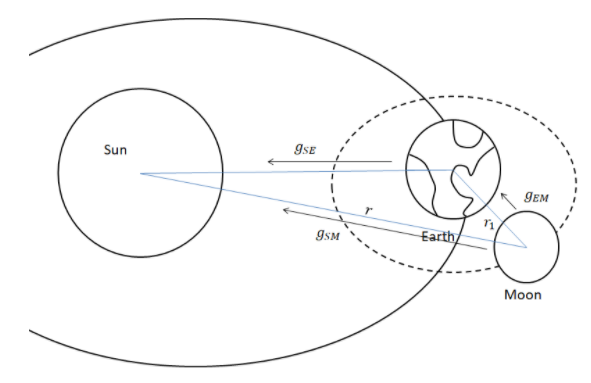
For the Sun-Moon system,
The force between Sun-Moon is, ${{F}_{SM}}=\dfrac{G{{m}_{Sun}}{{m}_{Moon}}}{{{r}^{2}}}$. Here r is the distance between Sun and Moon. Hence, the gravity acting on moon due to sun, becomes ${{F}_{SM}}=\dfrac{G{{m}_{Sun}}{{m}_{Moon}}}{{{r}^{2}}}={{m}_{Moon}}{{g}_{SM}}$. Similarly, the force between Earth-Moon system is given by, ${{F}_{EM}}=\dfrac{G{{m}_{Earth}}{{m}_{Moon}}}{{{r}_{1}}^{2}}$, where $r_{1}^{{}}$is the distance between the Earth and Moon. We know very well, that this distance is very much less than r. The gravity acting on Moon due to Earth becomes, ${{F}_{EM}}=\dfrac{G{{m}_{Earth}}{{m}_{Moon}}}{{{r}_{1}}^{2}}={{m}_{Moon}}{{g}_{EM}}$.
As given in the question, ${{F}_{SM}}=2{{F}_{EM}}$. Therefore, ${{m}_{Moon}}{{g}_{SM}}=2{{m}_{Moon}}{{g}_{EM}}\Rightarrow {{g}_{SM}}=2{{g}_{EM}}$.
Hence, the gravity pull with which the Moon is pulled by the Sun is twice that of the gravitational pull between Earth and Moon. What we must also understand is that almost the same amount of gravity acts on Earth due to the Sun, that is ${{g}_{SE}}\approx {{g}_{SM}}$.
All the planets and the natural satellites such as the moon revolve around the Sun due to the gravitational pull of the Sun. However, the revolving motion of the planets causes a stationary orbit or an orbit of constant energy. Due to this, all the planets stay in their orbits instead of spiraling into the Sun. However, the Moon doesn’t only revolve around the Sun but also around the Earth, because the Moon is within the Earth’s Roche sphere.
The Roche sphere is an imaginary sphere around a planet, within which the planet’s gravitational potential overpowers any other gravitational power until given enough energy to generate the escape velocity for the satellite. Hence, since the Moon falls within the Roche sphere of Earth, similar to other man-made satellites in space, the gravitational pull of earth overpowers that of the Sun.
Hence, Option D is the solution.

Note: The options B and C are true in concept however, neither of these options is the reason behind the Moon not being able to escape the Earth’s gravitational influence.
We know that the escape velocity is direction-dependent since velocity is a vector quantity, since the body is trying to escape the gravitational pull, it will always be away from the body pulling it. Hence option A is false.
Similarly, since earth and moon aren’t physically in contact or neither in contact with each other through any physical medium, hence both Option B and C are incorrect as well.
Option B states that less escape velocity is required by a body since it will already have initial kinetic energy due to the earth rotation.
The option C states that the earth’s rotation is anticlockwise, hence throwing the body towards the east direction will impart additional kinetic energy due to the earth’s rotation.