Question

The gravitational field in a region is $\vec{E} = (2\hat{i} +3\hat{j})\;Nkg^{-1}$. The equation for equipotential line is:
A.2x+3y=c
B.2y+3x=c
C.X+2y=c
D.1.5x+2y=c

Answer 1

Recall that the equipotential line traces all point at the same gravitational potential. This means that the equipotential line is perpendicular to the gravitational field lines. From this perspective, find the slope of the field vector given to us. Then, find the corresponding slope of the equipotential line by taking the negative reciprocal of the slope of the field vector. Then substitute this into the straight line equation and you should arrive at the equipotential line equation.
Formula Used:
Slope of a line perpendicular to a line of slope m: $m^{\prime} = -\dfrac{1}{m}$
Equation of a straight line: $y = mx+c$

Complete answer:
We know that an equipotential line is the line along which the gravitational potential is constant. They provide a quantitative way of viewing the gravitational potential in two dimensions. Every point on this line will be at the same potential. In three dimensions, the lines from equipotential surfaces. Moving along an equipotential surface requires no work because this movement is always perpendicular to the gravitational field.
Let the equation of the equipotential line be $y = mx+c$, where m is the slope of the line, c is the y-intercept, and y and x denote the directional y and x axes respectively.
We know that the equipotential line is always perpendicular to the gravitational field lines.

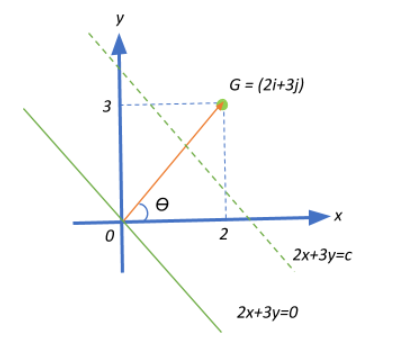
Given that $\vec{G} = (2\hat{i} +3\hat{j})\;Nkg^{-1}$ as shown in the diagram, we can calculate the slope of this vector, given by:
$tan\theta =\dfrac{3}{2}$.
Now, since the equipotential line will be perpendicular to the gravitational field, the slope of the equipotential line will be the negative reciprocal of the slope of the gravitational field vector, i.e.,
$m = -\dfrac{1}{tan\theta} = -\dfrac{1}{\dfrac{3}{2}} = -\dfrac{2}{3}$
Substituting this into our equipotential line equation:
$y = -\dfrac{2}{3}x+c \Rightarrow 3y=-2x+c \Rightarrow 2x+3y=c$

Therefore, the correct choice would be A. $2x+3y=c$

Note:
Note that though we got only one equation for the equipotential line, by varying the value of c we can get an infinite number of equipotential lines that are all perpendicular to the gravitational field. Thus, there is not one but many equipotential lines that are obtained for a given range of gravitational fields.