Question
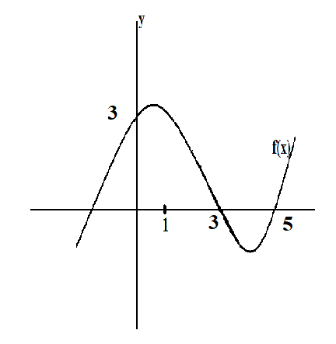
Question: The graph of \(y = f\left( x \right)\) is shown. Which is the graph of \(g\left( x \right) = 2f\left...
The graph of y=f(x) is shown. Which is the graph of g(x)=2f(x−2)+1?
A.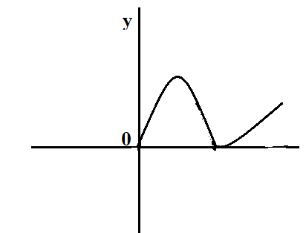
B. 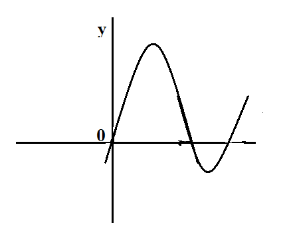
C. 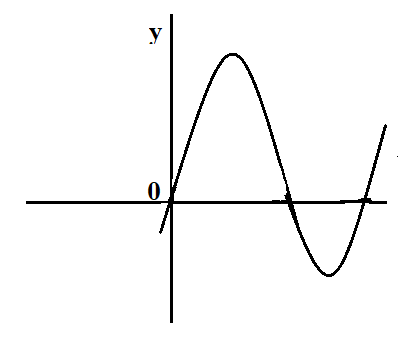
D. 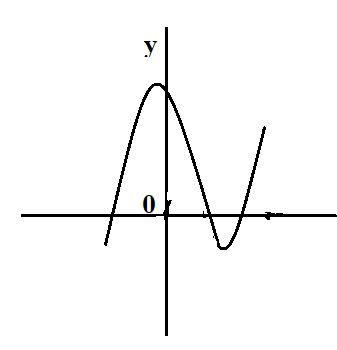
E. 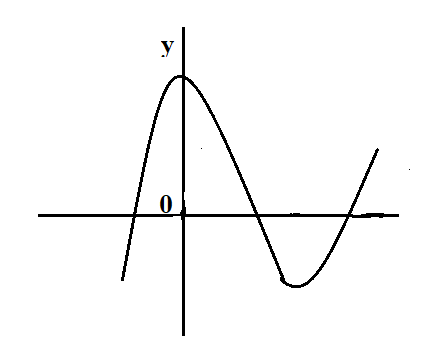
Solution
We are given the graph of the function y=f(x). Then, we can apply rules of transformations of graphs to find the graph of g(x)=2f(x−2)+1. We will also find how the coordinate changes for the same value in both the functions. Next, we will match from the given options, and select the graph which will satisfy all the transformations.
Complete step-by-step answer:
From the graph, we can see that the graph intersects the y axis at (0,3) and the graph also intersects the x axis at (3,0) and (5,0)
We can also find the value of g(x) by substituting the values 5 in the g(x)=2f(x−2)+1
Then,
g(5)=2f(5−3)+1 ⇒g(5)=2f(2)+1 ⇒g(5)=2(0)+1 ⇒g(5)=1
That is the point (5,0) shifted to (5,1)
Since, we have f(x−2), then its graph will shift to the right by 2.
And also the graph of 2f(x−2) will be stretched by 2.
Now, 1 is also added, then the graph will be moved upwards by 1 unit.
The function g(x)=2f(x−2)+1 can be obtained by moving the graph of y=f(x) to the right by 2 and also multiply the graph of y=f(x) by 2. Also, the graph will move upwards by 1 unit.
Hence, option B is the correct answer.
Note: If we have the graph of y=f(x), then the graph of f(x−k) shifts f(x) to the right by k units, the graph of kf(x) stretches vertically by k units if k>1 and shrinks by k units if 0<k<1. But if we have f(kx), then the graph of f(x) stretches horizontally by k units if k>1 and shrinks by k units if 0<k<1. The graph of f(x)+k can be obtained by shifting the graph of f(x) upwards by k units.
