Question

The graph of the sine function lies exactly in which of the following region?
A) $y = - 1{\text{ }}to{\text{ }}y = 1$
B) $y = - \infty {\text{ }}to{\text{ }}y = \infty {\text{ }}$
C) $y = 1{\text{ }}to{\text{ }}y = \infty {\text{ }}$
D) $y = - \infty {\text{ }}to{\text{ }}y = - 1$

Answer 1

Hint : To find the region in which graph of sine function lies exactly we will draw a graph by plotting various sine angles. From there, the maximum and minimum values on the y – axis will be the region or range of the sine function.
Trigonometric formulas:
$\sin \left( {90 + \theta } \right) = \cos \theta$
$\sin \left( {180 + \theta } \right) = - \sin \theta$

Complete step by step solution:
The value of different angles of sine is given as:
sin 0° = 0
sin 90° = 1
sin 180° = sin (90 + 90°)
= cos 90° $\left[ {\because \sin \left( {90 + \theta } \right) = \cos \theta } \right]$
= 0
sin 270° = sin (180 + 90°)
= sin 90° $\left[ {\because \sin \left( {180 + \theta } \right) = - \sin \theta } \right]$
= -1
sin 360° = sin (180 + 180°)
= sin 180°
= 0
To get a graph for sine function we can plot the values of certain angles on the graph. The table for values of sine can be drawn as:

Angles	Measure
sin 0°	0
sin 90° $\to \left[ {\sin \left( {\dfrac{\pi }{2}} \right)} \right]$	1
sin 180° $\to \left[ {\sin \left( \pi \right)} \right]$	0
sin 270° $\to \left[ {\sin \left( {\dfrac{{3\pi }}{2}} \right)} \right]$	-1
sin 360° $\to \left[ {\sin \left( {2\pi } \right)} \right]$	0

Plotting these values on graph we get:

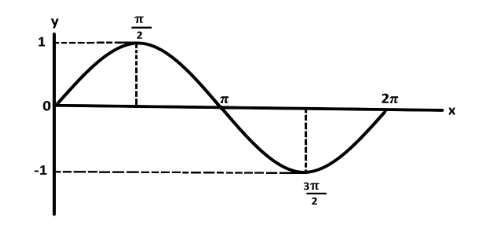
From the graph, it can be seen that the minimum value at y –axis is -1 and the maximum value is 1. So, the graph of sine function will lie between the range $y = - 1{\text{ }}to{\text{ }}y = 1$.
So, the correct answer is “Option A”.

Note : We take the sine angle greater than 180° with a negative sign because the value does not lie in the second quadrant and the sine function is positive only in the second quadrant where values lie between 90° to 180° .
We know that the value of sine function lies between the interval -1 to 1 and represented as:
$- 1 \leqslant \sin x \leqslant 1$
So, we could have written the range along y- axis directly