Question

The graph of the hyperbolic tangent function for all real values is:
A. Strictly increasing
B. Strictly decreasing
C. Strictly increasing in the interval [0,∞) and Strictly decreasing in the interval (-∞,0]
D. Strictly increasing in the interval (-∞,0] and Strictly decreasing in the interval [0,∞)

Answer 1

The hyperbolic tangent function,that is, ${\text{tanh}}$ function is the ratio of $\sinh$ function to the $\cosh$ function. We can find the trend of the graph by giving different values of x and observing the corresponding trend in y value.

Complete step by step answer:

The tanh function or hyperbolic tangent function is the ratio between hyperbolic sine and hyperbolic cosine.
We know that,
${\text{sinhx = }}\dfrac{{{{\text{e}}^{\text{x}}}{\text{ - }}{{\text{e}}^{{\text{ - x}}}}}}{{\text{2}}} \\\ {\text{coshx = }}\dfrac{{{{\text{e}}^{\text{x}}}{\text{ + }}{{\text{e}}^{{\text{ - x}}}}}}{{\text{2}}} \\\$
Then tanh is given by,
${\text{tanhx = }}\dfrac{{{\text{sinhx}}}}{{{\text{coshx}}}}{\text{ = }}\dfrac{{{{\text{e}}^{\text{x}}}{\text{ - }}{{\text{e}}^{{\text{ - x}}}}}}{{{{\text{e}}^{\text{x}}}{\text{ + }}{{\text{e}}^{{\text{ - x}}}}}}$
For ${\text{x = 0,tanhx = 0}}$.
As x increases, value of ${\text{tanhx}}$ also increases,
Also, as x decreases, the value of ${\text{tanhx}}$ decreases.

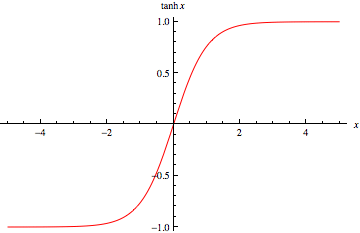
So, we can say that the graph of the hyperbolic tangent function is strictly increasing.
Therefore, the correct answer is option A.

Note: It is important to know the graph of the basic functions and how the value varies as x varies. Even though the graph is strictly increasing, the value of the function tends to 1 as x tends to infinity and -1 as x tends to negative infinity. This can be proved by taking the limits,
$\mathop {\lim }\limits_{x \to \infty } \tanh x = \mathop {\lim }\limits_{x \to \infty } \dfrac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} \\\ = \dfrac{{\mathop {\lim }\limits_{x \to \infty } \left( {1 - {e^{ - 2x}}} \right)}}{{\mathop {\lim }\limits_{x \to \infty } \left( {1 + {e^{ - 2x}}} \right)}} \\\ = \dfrac{{1 - \mathop {\lim }\limits_{x \to \infty } {e^{ - 2x}}}}{{1 + \mathop {\lim }\limits_{x \to \infty } {e^{ - 2x}}}} \\\ = \dfrac{1}{1} \\\ = 1 \\\$
Similarly, tanh tends to -1 when x tends to negative infinity. So the becomes almost straight at higher and lower values of x.