Question

The graph of the equation y=mx is a line which always passes through
$\begin{aligned} & \left( a \right)\left( 0,m \right) \\\ & \left( b \right)\left( x,0 \right) \\\ & \left( c \right)\left( 0,x \right) \\\ & \left( d \right)\left( 0,0 \right) \\\ \end{aligned}$

Answer 1

Hint: To solve the question given above, we will first find out what is a line and what is the variable m in the above equation. Then, we will check each option one by one and we will put values of x and y according to options. The values of x and y at which LHS will be equal to RHS will be the answer of this question.

Complete step-by-step answer:
Before solving the equation, we must know what is a line. A line can be defined as the figure formed by placing three or more points such that the area between any three points is zero. The general form of a straight line is $ax+by+c=0.$ The m given in the equation is the slope of the line. The slope is the inclination with respect to the x-axis in the anti-clockwise direction. The equation of straight line given in question is:
$y=mx$
Now, to find the point through which it passes, we will check each option one by one. The values of x and y at which the equation of line will have LHS and RHS equal will lie on the line.
Option(a): (0,m): We will put 0 in place of x and m in place of y. Thus, we will get:
$\begin{aligned} & m=m\left( 0 \right) \\\ & \Rightarrow m=0 \\\ \end{aligned}$
We can see that LHS$\ne$RHS so this point does not line or the line does not pass through this point.
Option(b):(x,0): We will put x in place of x and 0 in place of y. Thus, we will get:
$\begin{aligned} & 0=m\left( x \right) \\\ & \Rightarrow 0=mx \\\ \end{aligned}$
We can see that LHS$\ne$RHS so the line does not pass through this point.
Option(c):(0,x): We will put 0 in place of x and x in place of y. Thus, we will get;
$\begin{aligned} & x=m\left( 0 \right) \\\ & \Rightarrow x=0 \\\ \end{aligned}$
LHS$\ne$RHS so the line does not pass through this point.
Option(d):(0,0): We will put 0 in place of both x and y. Thus, we will get:
$\begin{aligned} & 0=m\left( 0 \right) \\\ & \Rightarrow 0=0 \\\ \end{aligned}$
LHS=RHS, so the line passes through this point.
Hence option (d) is correct.

Note: The alternate solution of the question is as follows. The general equation of a line can be represented by: $y=mx+c.$ In our case the equation of line is y=mx. This means that c=0. The c is the y intercept of the equation of line so (0,c) satisfies the equation of line. In other words we can say that the line passes through point (0,c).

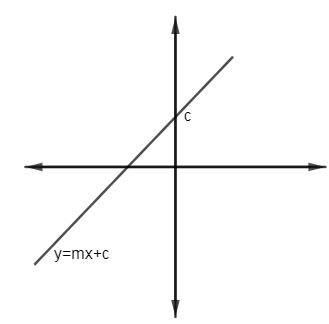
But, in our case, c=0 so the line will pass through (0,0).