Question
Question: The graph of radial component of E as a function of r will be: 
(A). 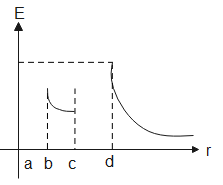
(B). 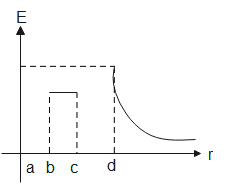
(C). 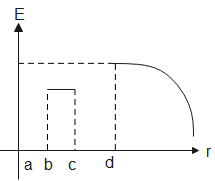
(D). 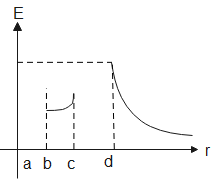
Solution
Figure contains two shells with inner radius and outer radii and the graphs depict a relationship between electric field due to the shells and the distance from the centre. The electric field depends on the charge enclosed and the distance from the centre of a shell. As the whole charge Is concentrated on the surface, the electric field inside the shell is zero.
Complete answer:
Electric field is the work done to bring a unit charge from infinity to a point in the field. Its SI unit is Cm2. It is given by-
E=4πε0r2q - (1)
Here, E is the electric field
q is the charge on the conductor
ε0 is the absolute permittivity
r is the distance from the conductor
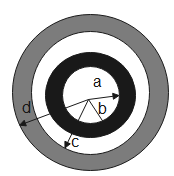
The electric field inside a conductor is therefore, for r<a, E=0
When we draw a Gaussian surface with radius a, the charge enclosed inside the Gaussian surface is zero.
Therefore, from eq (1),
q=0∴E=0
Therefore, for r < a, E=0.
For a < r < b, there is no charge present inside a conducting shell as all the charge is concentrated on the surface. Thus, the electric field inside a conducting shell is zero.
Therefore, for a < r < b, E=0.
For bE∝r21
Therefore, for b < r < c, the electric field is inversely proportional to the square of distance from the centre
Again, for c < r < d, the electric field inside the shell is zero as there is no charge inside a conducting shell.
Therefore, for c < r < d, E=0
For dTherefore, for d < r, the electric field is inversely proportional to the radial component.
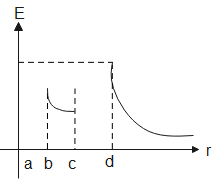
Therefore, the electric field is zero for r < a, a < r < b, c < r < d and is inversely proportional to the radial component for b < r < c, d < r.
Hence the correct graphical representation is (A).
Note:
A Gaussian surface is an imaginary surface through which the electric lines of forces pass through normally. According to the Gauss law, the flux is equal to the charge enclosed in a Gaussian surface divided by absolute permittivity of free space. Question might arise for why is the electric field zero for r
