Question
Question: The graph of magnification v/s image distance of a thin lens is given its focal length will be- \[...
The graph of magnification v/s image distance of a thin lens is given its focal length will be-
& A.~~~~~~~~~~~~~f=-\dfrac{a}{c} \\\ & B.~~~~~~~~~~~~~f=\dfrac{b}{c} \\\ & C.~~~~~~~~~~~~~f=-\dfrac{c}{b} \\\ & D.~~~~~~~~~~~~None\text{ }of\text{ }these \\\ \end{aligned}$$ 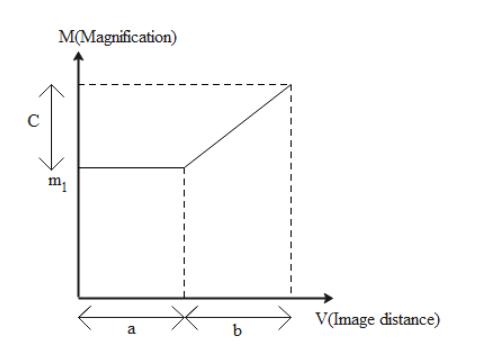Solution
We are given magnification v/s image distance, as it is a straight line we can use it to find magnification as a function of image distance. We can also get the relation between magnification and image distance in terms of focal length and can use it to find Focal length in terms of a, b and c .
Formula Used :
Lens Formula
v1−u1=f1 … (1)
m=uv … (2)
where v is image distance, u is object distance, m is magnification and f is focal length.
Complete step-by-step answer :
By lens formula we have,
v1−u1=f1
u1=v1−f1
Using the value of u1 from above equation and putting it in equation 2,
m=uv=v[v1−f1]
m=1−fv
From the above equation slope of graph must be;
−f1
From the graph we can see that slope of AB=ACBC
Now as BC=c and AC=b, So
AB = c/b
−f1=bc
f=−bc
Hence the correct option is C.
Note :The formula of magnification changes to m=uv for lens. The formula m=−uv is applicable only in the mirror. All the formulas of a mirror can be applied in a lens by replacing u with –u. If both b and c will be positive or negative, focal length of lens will be negative meaning this is drawn for a concave lens but if only one of them is negative, the lens is convex. However this interpretation is true only when the lens is kept in the surrounding having refractive index less than the refractive index of the lens.
