Question

The graph of Kinetic Energy (K) of a body versus velocity (v) is represented as
(A) Hyperbola
(B) Parabola
(C) Straight line
(D) None of these

Answer 1

Hint
The kinetic energy of a body moving in a straight line is directly proportional to the square of its velocity. This also implies that it has a graph whose slope is not constant.
Formula used: $K = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the body and $v$ is the velocity of its motion.

Complete step by step answer
Firstly, let us write down the formula for kinetic energy
$\Rightarrow K = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the body and $v$ is the velocity of its motion.
For a graph of $K$ versus $v$, $K$ is analogous to $y$ and $v$ is analogous to $x$.
Thus, can be written representatively as $y = a{x^2}$ where $a$ is a constant equal to $\dfrac{1}{2}m$.
Now, we compare each of the types of graph given in the option
First, the hyperbola:
The algebraic equation of a hyperbola centered at the origin is given as:
$\Rightarrow \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ where $a$ and $b$ are constants.
Comparing this equation to $y = a{x^2}$ it can be observed that no form of algebraic manipulation will make them the same since the variable $y$ doesn’t have the same exponent. Thus, we can rule it out.
Next, we compare it to that of a parabola:
Equation of a parabola at the origin can be given as:
$\Rightarrow y = 4p{x^2}$ where $p$ is a constant
Comparing this to equation $y = a{x^2}$, we can see that they are identical if we make $a = 4p$. Thus, the equations are both equations of a parabola. In fact, $y = 4p{x^2}$ is only called the focal point form while $y = a{x^2}$ is called the Cartesian form.
The equation of a straight line is $y = ax$. Comparing this with $y = a{x^2}$ we also see that the exponent of $x$ is not the same in the two equations. Thus, can be ruled out.
Therefore, we can conclude that the graph of kinetic energy versus velocity is represented by a parabola.
Hence, the correct option is B.

Note
Alternatively, we can actually compare the graphs each with a sketch of $K$ against $v$.
A quick sketch of $K$ against $v$ will give something similar to the graph below

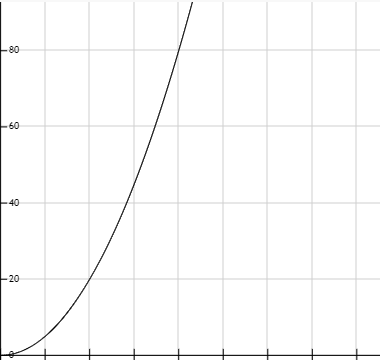
For hyperbola:

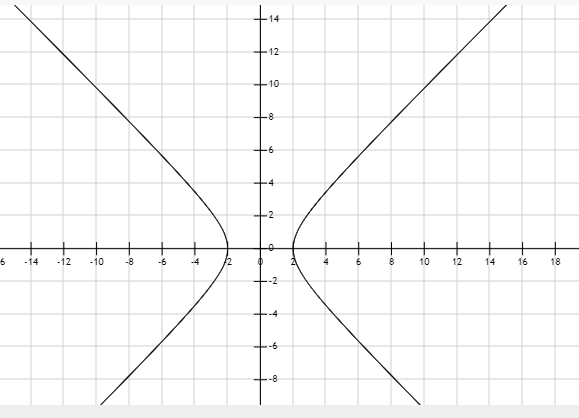
For parabola:

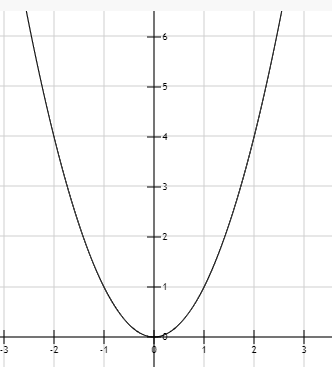
And for straight line:

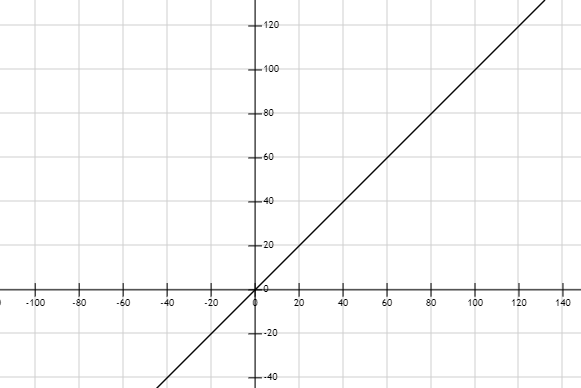
Comparing the graphs with the sketch of kinetic energy, we see that the most matching graph is that of the parabola but with the x-axis cut off.