Question

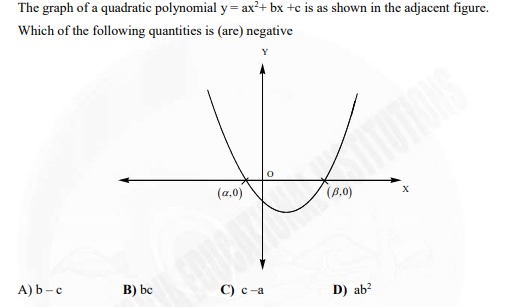
The graph of a quadratic polynomial y = ax²+ bx +c is as shown in the adjacent figure. Which of the following quantities is (are) negative

• A. b – c
• B. bc
• C. c – a
• D. ab²

Answer 1

Answer: (C)

c – a

Answer 2

From the graph of the quadratic polynomial $y = ax^2 + bx + c$, we determine the signs of the coefficients $a$, $b$, and $c$.

• The parabola opens upwards, so $a > 0$.
• The y-intercept is at $(0, c)$, and it is below the x-axis, so $c < 0$.
• The x-coordinate of the vertex is $-\frac{b}{2a}$, and it is positive from the graph. Since $a > 0$, we have $-b > 0$, which means $b < 0$.

So, we have $a > 0$, $b < 0$, and $c < 0$.

Now we check the signs of the given quantities:

A) $b - c$: Since $b$ and $c$ are both negative, the sign of $b - c$ depends on their relative magnitudes. It can be positive or negative. B) $bc$: Since $b < 0$ and $c < 0$, $bc = (-ve) \times (-ve) = +ve$. C) $c - a$: Since $c < 0$ and $a > 0$, $c - a = (-ve) - (+ve) = (-ve) + (-ve) = -ve$. D) $ab^2$: Since $a > 0$ and $b < 0$, $b^2 > 0$. So $ab^2 = (+ve) \times (+ve) = +ve$.

Therefore, the only quantity that is always negative is $c - a$.