Question

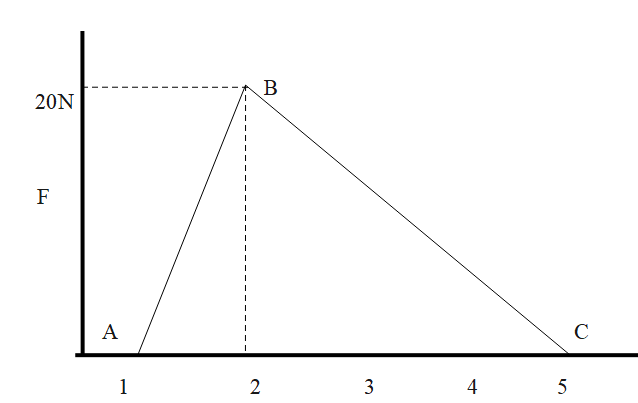
The graph between the resistive force F acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 25kg and initial velocity is 2mps. Find the kinetic energy when the body has travelled 2m and 5m.

Answer 1

In the above question, we are given all the parameters that are needed to find the initial kinetic energy of the body. As there is some resistive force, the work done against resistive force must also be calculated. The final kinetic energy would be the difference between the initial kinetic energy and the work done against resistive force.

Complete step by step answer:
Let us first write the given terms,
The mass of the body is 25kg, the velocity initially is 2mps. We need to find the initial kinetic energy of the body.
The initial kinetic energy can be calculated as,
$\dfrac{1}{2}m{{v}^{2}}$
Now, the initial kinetic energy of the body will be
$\begin{aligned} & KE=\dfrac{1}{2}\times 25\times 4 \\\ & \Rightarrow KE=50J \\\ \end{aligned}$
Now, we need to find the work done against resistive force when the object travelled for 2m and 5m.
$\begin{aligned} & {{W}_{2m}}=\dfrac{1}{2}\times b\times h \\\ & \Rightarrow {{W}_{2m}}=\dfrac{1}{2}\times 1\times 20 \\\ & \therefore {{W}_{2m}}=10J \\\ \end{aligned}$
Similarly, when the body travels 5m, it is,
$\begin{aligned} & {{W}_{5m}}=10J+\dfrac{1}{2}\times b\times h \\\ & \Rightarrow {{W}_{5m}}=10J+30J \\\ & \therefore {{W}_{5m}}=40J \\\ \end{aligned}$
Now, the final kinetic entry will be the difference between initial kinetic energy and the work done against resistive force.
$\begin{aligned} & {{(K{{E}_{f}})}_{2m}}=50J-10J=40J \\\ & \therefore {{(K{{E}_{f}})}_{5m}}=50J-40J=10J \\\ \end{aligned}$
Hence, in this way, we can calculate the kinetic energy of a body when there’s some resistive force acting on it.

Additional information:
Kinetic energy is the energy an object has because of its motion.
If we want to accelerate an object, then we must apply a force. Applying a force requires us to do work. After work has been done, energy has been transferred to the object, and the object will be moving with a new constant speed. The energy transferred is known as kinetic energy, and it depends on the mass and speed achieved. Kinetic energy can be transferred between objects and transformed into other kinds of energy. For example, a flying squirrel might collide with a stationary chipmunk. Following the collision, some of the initial kinetic energy of the squirrel might have been transferred into the chipmunk or transformed to some other form of energy.

So, the correct answer is “Option B”.

Note:
In the above question, the graph relates the resistive force acting and the distance travelled by the body. As the kinetic energy needs to be calculated, the energy equivalent of the force, or the work done by the resistive force can be calculated by finding their area under the graph displayed.