Question

The graph between stopping potential ($V_0$) versus frequency ($\nu$) of the light used in an experiment of photoelectric effect is as shown in figure. Work function of the metal surface is

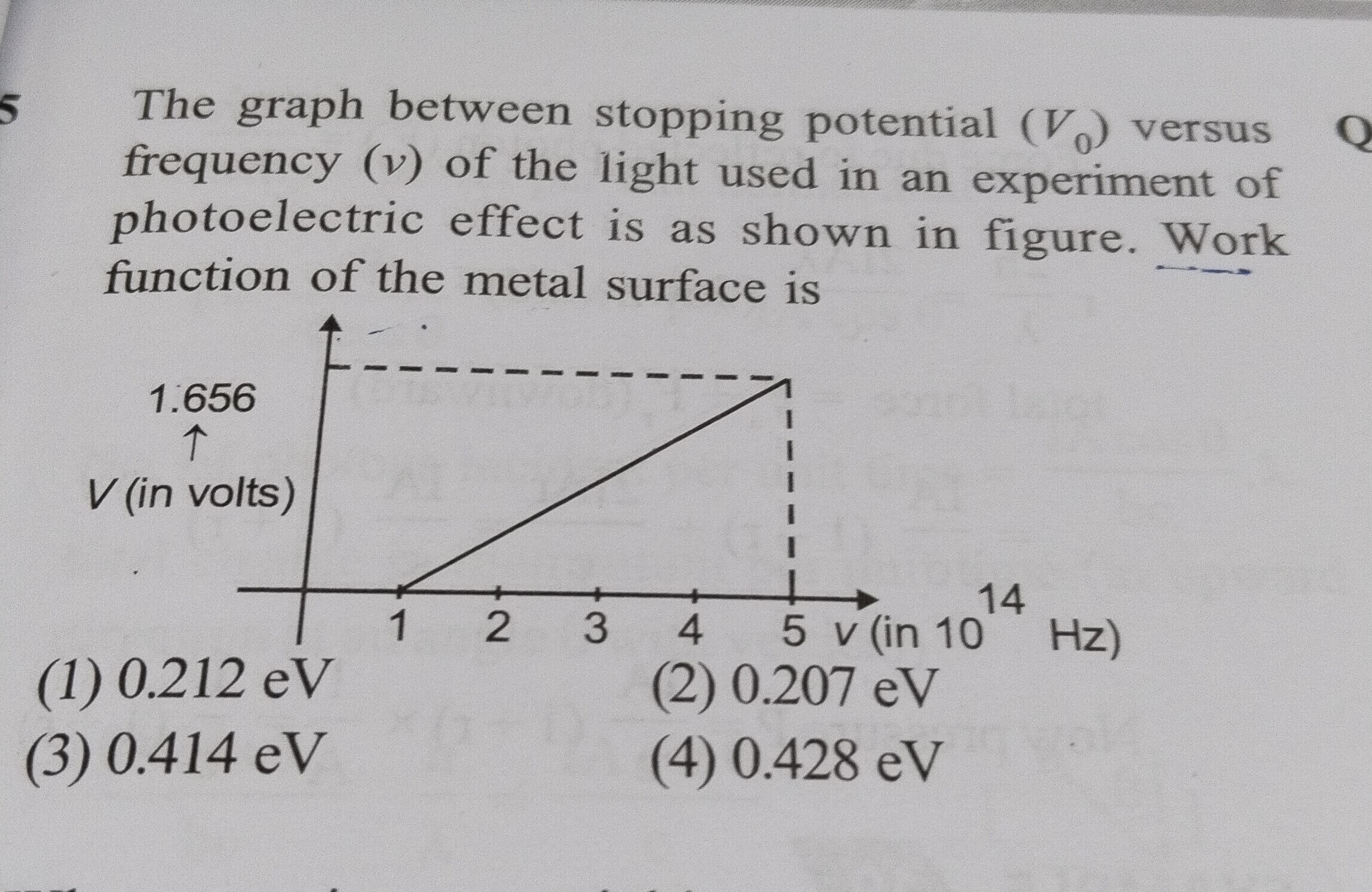
• A. 0.212 eV
• B. 0.207 eV
• C. 0.414 eV
• D. 0.428 eV

Answer 1

Answer: (C)

0.414 eV

Answer 2

The relationship between stopping potential ($V_0$) and frequency ($\nu$) in the photoelectric effect is given by Einstein's photoelectric equation:

$h\nu = \phi + K_{max}$

where $h$ is Planck's constant, $\phi$ is the work function, and $K_{max}$ is the maximum kinetic energy of the emitted photoelectrons. The maximum kinetic energy is also related to the stopping potential ($V_0$) by:

$K_{max} = eV_0$

where $e$ is the elementary charge.

Substituting $K_{max}$ into the photoelectric equation:

$h\nu = \phi + eV_0$

Rearranging the equation to express $V_0$:

$eV_0 = h\nu - \phi$ $V_0 = \left(\frac{h}{e}\right)\nu - \left(\frac{\phi}{e}\right)$

This equation is in the form of a straight line, $y = mx + c$, where:

• $y = V_0$ (stopping potential)
• $x = \nu$ (frequency)
• The slope $m = \frac{h}{e}$
• The y-intercept $c = -\frac{\phi}{e}$

From the graph, we can determine the work function ($\phi$) using the threshold frequency ($\nu_0$). The threshold frequency ($\nu_0$) is the minimum frequency of incident light required for photoemission to occur. At this frequency, the stopping potential ($V_0$) is zero.

From the photoelectric equation, when $V_0 = 0$:

$h\nu_0 = \phi$

The graph shows that the line intersects the frequency axis (where $V_0 = 0$) at $\nu = 1 \times 10^{14}$ Hz. So, the threshold frequency $\nu_0 = 1 \times 10^{14}$ Hz.

Now, we can calculate the work function:

$\phi = h\nu_0$

Using Planck's constant $h = 6.626 \times 10^{-34}$ J s:

$\phi = (6.626 \times 10^{-34} \text{ J s}) \times (1 \times 10^{14} \text{ Hz})$ $\phi = 6.626 \times 10^{-20}$ J

To express the work function in electron volts (eV), we divide by the elementary charge $e = 1.602 \times 10^{-19}$ J/eV:

$\phi = \frac{6.626 \times 10^{-20} \text{ J}}{1.602 \times 10^{-19} \text{ J/eV}}$ $\phi \approx 0.4136 \text{ eV}$

Rounding to three significant figures, $\phi \approx 0.414 \text{ eV}$.