Question

The graph between$\dfrac{1}{\lambda }$ and stopping potential $(V)$ of three metals having work functions ${{\phi }_{1,}}{{\phi }_{2}}$ and ${{\phi }_{3}}$ in an experiment of photo-electric effect is plotted as shown in the figure. Which of the following statement(s) is/are correct?[ Here $\lambda$ is the wavelength of the incident ray].

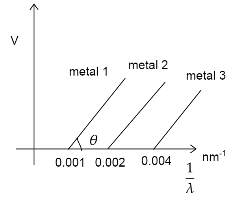
A. Ratio of work functions ${{\phi }_{1}}:{{\phi }_{2}}:{{\phi }_{3}}=1:2:4$
B. Ratio of work functions ${{\phi }_{1}}:{{\phi }_{2}}:{{\phi }_{3}}=4:2:1$
C.$\tan \theta$ is directly proportional to $\dfrac{hc}{e}$ ,where $h$ is Planck’s constant and $c$ is the speed of light.
D. The violet colour light can eject photoelectrons from metal $2$ and $3$

Answer 1

Here we will use Einstein’s photoelectric equation. From that equation we will see how the graph between stopping potential and $\dfrac{1}{\lambda }$ gives information about different parameters. From that information we will be able to answer the question. We follow these steps to answer the question.

Formula used: ${{V}_{0}}=(\dfrac{hc}{e})\dfrac{1}{\lambda }-(\dfrac{hc}{e})\dfrac{1}{{{\lambda }_{0}}}$

Complete step by step answer:
If ${{V}_{0}}$ is the stopping potential,$\lambda$ is the wavelength of the incident light and${{\lambda }_{0}}$ is the threshold wavelength then Einstein’s photoelectric equation can be re written as
${{V}_{0}}=(\dfrac{hc}{e})\dfrac{1}{\lambda }-(\dfrac{hc}{e})\dfrac{1}{{{\lambda }_{0}}}.....(1)$
If we compare this equation with the equation of a straight line
$y=mx+c$ then we can see the slope of the graph $m=(\dfrac{hc}{e})$ . Now from the question the slope of the graph is $\tan \theta$ , so $\tan \theta =\dfrac{hc}{e}$ .
Thus the option C is correct.
Again the equation $(1)$ can be re written as
$e{{V}_{0}}=\dfrac{hc}{\lambda }-\phi ........(2)$ , where $\phi$ is the work function of the metal. Now when ${{V}_{0}}=0$ , we can write from $(2)$
$\begin{aligned} & \phi =\dfrac{hc}{\lambda } \\\ & or\phi \propto \dfrac{1}{\lambda } \\\ \end{aligned}$
Now from the graph we have
$\begin{aligned} & \dfrac{1}{{{\lambda }_{1}}}:\dfrac{1}{{{\lambda }_{2}}}:\dfrac{1}{{{\lambda }_{3}}}=0.001:0.002:0.004=1:2:4 \\\ & or{{\phi }_{1}}:{{\phi }_{2}}:{{\phi }_{3}}=1:2:4 \\\ \end{aligned}$
So the option A is correct.
Now violet has the wavelength
$\begin{aligned} & {{\lambda }_{v}}=380nm \\\ & or\dfrac{1}{{{\lambda }_{v}}}=0.0026n{{m}^{-1}} \\\ \end{aligned}$
Thus from the graph we can see $\dfrac{1}{{{\lambda }_{v}}}>\dfrac{1}{{{\lambda }_{2}}}$ and$\dfrac{1}{{{\lambda }_{v}}}<\dfrac{1}{{{\lambda }_{3}}}$, so violet light can eject electron from metal $2$ but not from metal $3$ .
So option D is also incorrect.

So, the correct answer is “Option A and C”.

Note: Here we need to know about the photoelectric effect. We need to modify Einstein's photoelectric equation in different forms according to the question to be answered. An incident radiation can only eject electrons from a metal if its frequency is greater than some minimum value called the threshold frequency.