Question

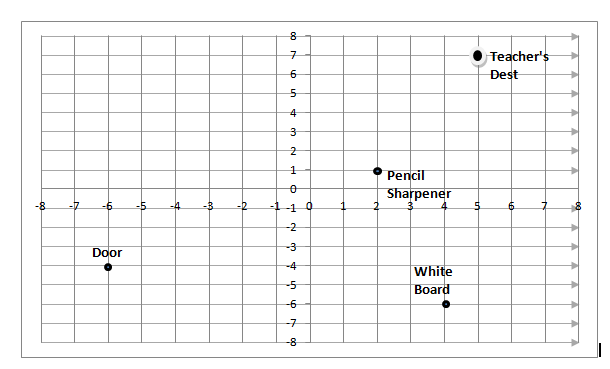
The graph below shows the place in the math classroom. Each unit presents $1$ foot. What is the distance, in feet, between the pencil sharpener and the door? Round your answer nearest to the tenth.

Answer 1

Here, we can get the distance between the pencil sharpener and the door by using the formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ , where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the coordination of the first object and $\left( {{x}_{2}},{{y}_{2}} \right)$ is the coordination of the second object. So, we will find out the coordinates of the pencil sharpener and the door respectively. Then we will get the distance by using the formula.

Complete step by step solution:
Since, we need to find the distance between the pencil sharpener and the door. So, we will use the formula for that we need the coordination of the pencil sharpener and the door.
Here, we already have the graph in which we can see the coordination of the pencil sharpener and the door as:
Coordination of the pencil sharpener $=\left( 2,1 \right)$
Because the point lies where it covers $2$ unit from y axis in the direction of x axis and covers $1$ unit from x axis in the direction of y axis.

Similarly, the coordination of the door $=\left( -6,-3 \right)$
Because the point lies where it covers $6$ unit from y axis in the negative direction of x axis and covers $3$ unit from x axis in the negative direction of y axis.

Here we got the coordination. So we will use the formula that is:
$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Here, we will consider the coordination of pencil sharpener $\left( {{x}_{1}},{{y}_{1}} \right)$ and coordination of door $\left( {{x}_{2}},{{y}_{2}} \right)$ and will use them in the above formula as:
$=\sqrt{{{\left( -6-2 \right)}^{2}}+{{\left( -3-1 \right)}^{2}}}$
Now, we will do addition for bracketed terms because they have same sign as:
$=\sqrt{{{\left( -8 \right)}^{2}}+{{\left( -4 \right)}^{2}}}$
Here, we will square them and will get positive value as:
$=\sqrt{64+16}$
Now, the sum of $64$ and $16$ is $80$ as:
$=\sqrt{80}$
Since, $80$ is not a perfect square no. So we will get the square root of $80$ as:
$=4\sqrt{5}$
Here, we can replace $\sqrt{5}$ by putting its value that is $2.236$ as:
$=4\times 2.236$
After doing multiplication we will have:
$=8.944$
Since, each unit presents $1$ foot. So, we don’t need any other calculation.
Hence, the distance, in feet, between the pencil sharpener and the door is $8.94$ feet.

Note: For this type of question where we need to find the distance between two points, we will use the formula of distance between two points that is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and where we can choose any one coordination of any point as $\left( {{x}_{1}},{{y}_{1}} \right)$ . So, we will choose any coordination as $\left( {{x}_{1}},{{y}_{1}} \right)$, normally other will be $\left( {{x}_{2}},{{y}_{2}} \right)$ itself.