Question

The given set $\left( A\cup B\cup C \right)\cap \left( A\cap {{B}^{'}}\cap {{C}^{'}} \right)\cap {{C}^{'}}$ is equal to:
(a) $B\cap {{C}^{'}}$,
(b) $A\cap C$,
(c) ${{B}^{'}}\cap {{C}^{'}}$,
(d) None of these.

Answer 1

We start solving the problem by drawing the Venn diagram of all the sets given. We recall the definition of union of sets A, B and C from the Venn diagrams. We then recall the definition of complement of sets and draw the Venn diagrams of ${{C}^{'}}$ and ${{B}^{'}}$.After drawing all the Venn diagrams, we check the common area of all the sets to find the required set.

Complete step-by-step answer :
According to the problem, we need to find which of the options is equal to the set $\left( A\cup B\cup C \right)\cap \left( A\cap {{B}^{'}}\cap {{C}^{'}} \right)\cap {{C}^{'}}$.
Let us draw the Venn diagrams to solve this problem. We have three different sets A, B and C or which Venn diagram looks as follows:

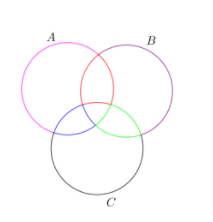
From the figure, we can see all the intersection and union of sets A, B and C clearly.
We know that intersection of two or more sets includes all the elements present in both sets. So, $A\cup B\cup C$ denotes elements in all the three sets.
We know that complement of any set is defined as the set of all elements in a given universal set except the given set.
We get ${{C}^{'}}$ as follows:

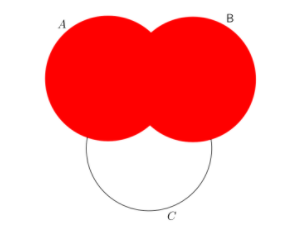
Similarly, we get ${{B}^{'}}$ as follows:

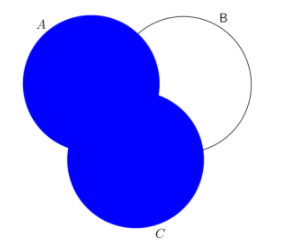
From these two figures, we can see that the intersection is the portion of set A that does not have any intersection with other sets.
So, we have got $A\cap {{B}^{'}}\cap {{C}^{'}}=\left( A\cup B\cup C \right)\backslash \left( B\cup C \right)$ which is ${{\left( BUC \right)}^{'}}$.
Now, we have to find the intersections of $\left( A\cup B\cup C \right)\cap \left( \left( A\cup B\cup C \right)\backslash \left( B\cup C \right) \right)$. We know that the intersection of two sets $A$ and $A\backslash {{B}^{'}}$ is $A\backslash {{B}^{'}}$.
So, we get the intersection of $\left( A\cup B\cup C \right)\cap \left( \left( A\cup B\cup C \right)\backslash \left( B\cup C \right) \right)$ as $\left( A\cup B\cup C \right)\backslash \left( B\cup C \right)$, which is ${{\left( BUC \right)}^{'}}$.
We know that ${{\left( A\cup B \right)}^{'}}={{A}^{'}}\cap {{B}^{'}}$. So, ${{\left( BUC \right)}^{'}}$ is ${{B}^{'}}\cap {{C}^{'}}$. From all the Venn diagrams, we can see that the intersection of ${{B}^{'}}\cap {{C}^{'}}$ and ${{C}^{'}}$ is ${{B}^{'}}\cap {{C}^{'}}$.
So, we have got the set $\left( A\cup B\cup C \right)\cap \left( A\cap {{B}^{'}}\cap {{C}^{'}} \right)\cap {{C}^{'}}$ equal to ${{B}^{'}}\cap {{C}^{'}}$.
The correct option for the given problem is (c).

Note : We should not confuse ${{\left( A\cup B \right)}^{'}}={{A}^{'}}\cap {{B}^{'}}$ with ${{\left( A\cup B \right)}^{'}}={{A}^{'}}\cup {{B}^{'}}$. We can find this result by using the formula $n\left( a\cup b\cup c \right)=n\left( a \right)+n\left( b \right)+n\left( c \right)-n\left( a\cap b \right)-n\left( b\cap c \right)-n\left( a\cap c \right)+n\left( a\cap b\cap c \right)$ wherever required and making subsequent calculations. It is easy to imagine about sets by drawing Venn diagrams and the answer can be found easily by just seeing from the Venn diagrams without any calculations. Similarly, we can expect problems with 3 or more sets.