Question
Question: The given graph shows variation of charge versus potential difference V for two capacitors \[{{C}_{1...
The given graph shows variation of charge versus potential difference V for two capacitors C1 and C2. Both the capacitors have the same plate separation but plate area of C2, is greater than that of C1. Which line (A or B) corresponds to C1 and C2 why?
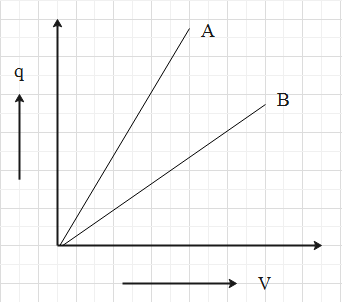
Solution
The problem is based on the concept of the capacitance of the capacitor. Using the formula for calculating the capacitance of the capacitor, and finding the relation between the capacitance and the area of the capacitor, this problem can be easily solved.
Formula used:
C=dε0A
Complete answer:
The capacitance of a capacitor is derived as follows.
The capacitance of a capacitor is directly proportional to the area of the parallel plates of a capacitor.
So, we have,
C∝A …… (1)
The capacitance of a capacitor is inversely proportional to the separation between the parallel plates of a capacitor.
So, we have,
C∝d1
Combine both the equations.
C∝dA
Thus, the capacitance of a capacitor is given by the formula as below.
C=dε0A
Where C is the capacitance, ε0 is the permittivity of dielectric, A is the cross-sectional area of the plates and d is the separation between the plates.
Now consider the separate equations for the two capacitors C1 and C2.
We have,
