Question
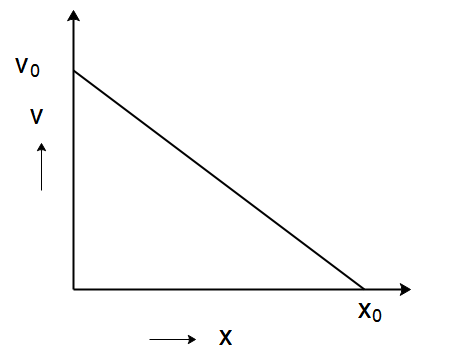
Question: The given graph shows the variation of velocity with displacement. Which one of the graphs given bel...
The given graph shows the variation of velocity with displacement. Which one of the graphs given below correctly represents the variation of acceleration with displacement?
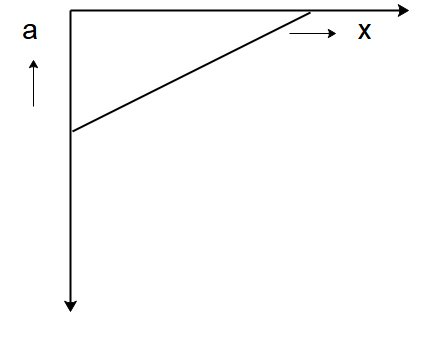
A)
B)
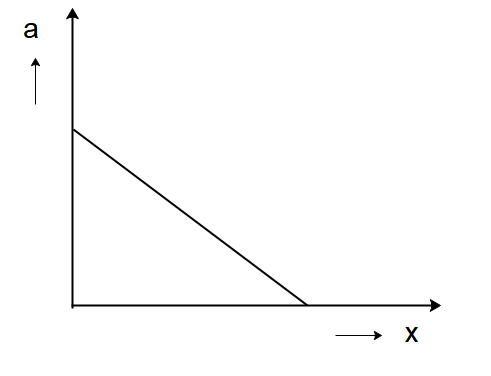
C)

D)
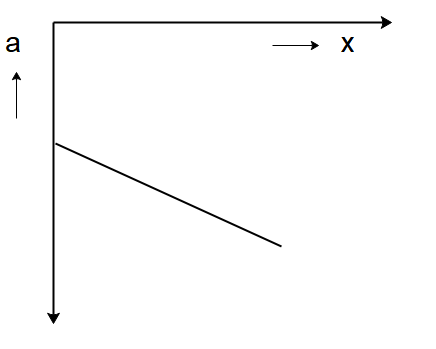
Solution
The velocity of the object is decreasing with increasing distance. We will determine the equation of motion for this motion and use the laws of motion to determine the variation of acceleration with displacement.
Complete step by step answer
In the graph given to us, we can see that the line intercepts the y -axis at v0. The slope of the line can be determined as the line passing through the points on the y -axis and the x -axis as
⇒m=x2−x1y2−y1
The two points of concern will be (x1,y1)=(0,v0) The x -coordinate will be zero since the point is on the y -axis.
And (x2,y2)=(x0,0) since the point is on the x -axis its y -coordinate is zero. So the slope of the line will be
⇒m=−x0v0
Then the equation of the line can be determined as
⇒y=mx+c where c is the y -intercept of the line. So, for the line in question, the equation will be
⇒v=−x0v0x+v0
Now the acceleration of the object will be
⇒a=dtdv and we can multiply the numerator and the denominator with dx and write
⇒a=dxdvdtdx
Substituting dtdx=v and v=−x0v0x+v0 in the above equation, we get
⇒a=(x0v0)2x−x0v02
This equation of acceleration a is again of the form y=mx+c where
⇒m=(x0v0)2 and c=−x0v02.
Since the y -intercept is negative and the slope of the line is positive the only option that matches this choice is option (A).
Note
We must be careful to derive the relation of acceleration with displacement as given in the option and not of acceleration with velocity. To do so, we must be familiar with the method to form the equation of a line from different points given to us.
