Question
Question: The given figure shows a wire sliding on two parallel conducting rails placed at a separation ‘l’. A...
The given figure shows a wire sliding on two parallel conducting rails placed at a separation ‘l’. A magnetic field B exists in a direction perpendicular to the plane of the rails. What is the force necessary to keep the wire moving at a Constant velocity v will be:
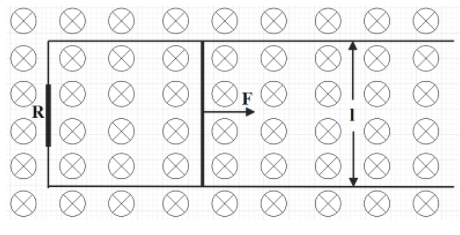
A)RB2l2vB)R2B2l2vC)2RB2l2vD)None of these
Solution
To solve this question, we will use the expression for magnetic Lorentz force. Also, we will need ohm’s law and faraday's law for induced emf to find the current induced in the circuit as there is change in magnetic field, which results in creating induced emf in a closed loop. Then, by substituting the expression for current in the Lorentz force equation, we can find the force.
Formula used:
F=Bilemf=Blvi=Remf
Complete step by step answer:
The force experienced by the wire while moving on the parallel conducting wire through the magnetic field is given by the equation,
