Question
Question: The given figure shows a part of an electrical circuit. The potentials at the points \(a,b\) and \(c...
The given figure shows a part of an electrical circuit. The potentials at the points a,b and c are 30V,12V and 2V respectively. Find the currents through the three resistors.
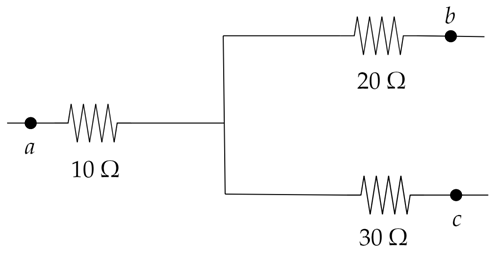
Solution
We have to consider the node as d and then suppose a potential of V exists there. As b and c are in parallel so the current from a splits up into two equal values. We have to assume a current is flowing in the circuit a. Then by comparing the equations with the help of Kirchhoff’s Law we will find the value of the unknown potential. After that we will be using Ohm’s Law to find the values of current.
Complete step by step solution:
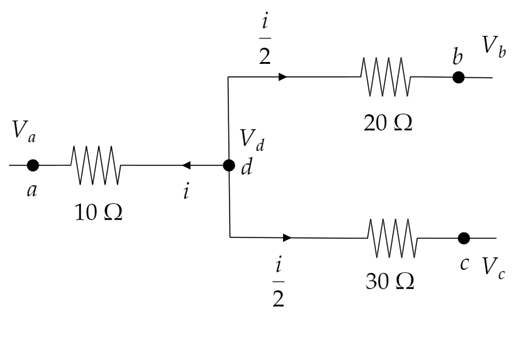
Let the potential at point d as shown in figure be Vd. Let a current i flows from a to d.
Since, d to b circuit and the d to c circuit are in parallel so both have the same current flowing through it.
It means that current i is being split up into two equal magnitudes of current 2i. So, 2i current is flowing through the parallel circuit.
The potentials at the points a,b and c are 30V,12V and 2V respectively.
So, Va=30V, Vb=12V and Vc=2V.
And the given resistances are, Ra=10Ω, Rb=20Ω and Rc=30Ω
Now applying Kirchhoff’s Law we get,
Va−Vd−(i×Ra)=0
⇒30−Vd=10i−−−−−(1)
Similarly,
Vd−12=20×2i=10i−−−−−(2)
Vd−2=30×2i=15i−−−−−(3)
Comparing equation (1) and (2) we get,
30−Vd=Vd−12
∴Vd=25
So, the potential at point d is 25V.
Now, we know that the currents flowing through resistances Ra, Rb and Rc is i, 2i and 2i respectively.
Now by using Ohm’s Law we get,
Va−Vd=i×R
30−25=i×10
So the value of i=0.5 A
Therefore, 2i=0.25 A.
So, the currents flowing through resistances Ra, Rb and Rc is 0.5 A, 0.25 A and 0.25 A.
Note: It must be noted that we must consider a common potential point in this type of question. As the potential at point d is greater than b and c so, the current flows outwards from d with respect to b and c but as the potential at point a is greater than d, the currents flows inwards or towards d.
