Question

The given apparatus shows a heavy piston supported by gas trapped in a cylinder. The cross-sectional area of the piston is $4.0 \times {10^{ - 4}}\;{{\text{m}}^2}$. The pressure of the gas inside the cylinder is $1.5 \times {10^5}\;{\text{Pa}}$ and the atmospheric pressure is $1.0 \times {10^5}\;{\text{Pa}}$. Find the mass of the piston.
(Take $g = 10\;{\text{m/}}{{\text{s}}^{\text{2}}}$ )
A) $1\;{\text{kg}}$
B) $2\;{\text{kg}}$
C) $3\;{\text{kg}}$
D) $4\;{\text{kg}}$

Answer 1

In this question, the concept of the pressure is used to calculate the mass of the piston that is pressure is the equal to the applied force per unit area of cross-section of the object and use the force equilibrium equation to obtain the result.

Complete step by step solution:
As we know that the pressure is equal to force per unit area and can be written as,
$\Rightarrow P = \dfrac{F}{A}$
Where, the applied force is $F$ and the area of cross-section is $A$.
And we also know that the force is also equal to the weight of the object which is the product of acceleration due to gravity and mass of the object and can be written as,
$\Rightarrow F = mg$
Here, the mass of the object is $m$ and the acceleration due to gravity is $g$.

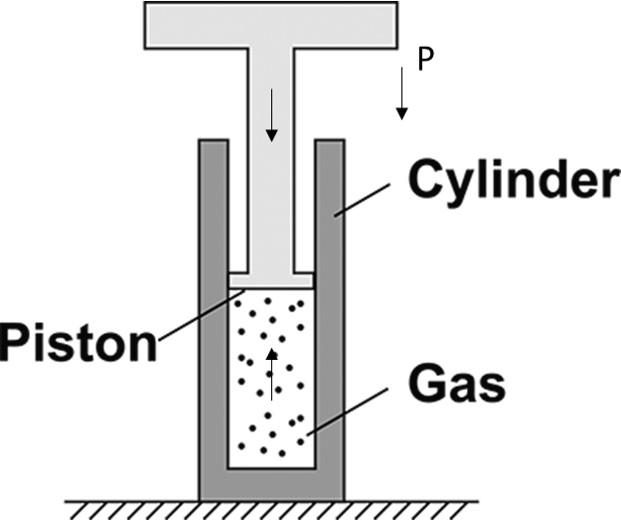
From the above diagram, we can understand, the piston is pushing the gas downwards along with the atmospheric pressure which is also in the downward direction. The pressure applied by the gas is in an upward direction.
Therefore, we can write,
$\Rightarrow {F_{gas}} = {F_{atmospheric}} + {F_p}......\left( 1 \right)$
Now, as we know that ${F_p} = mg$ and
$\Rightarrow P = \dfrac{F}{A}$
Now, we rearrange the above equation as,
$\Rightarrow F = PA$
Therefore, according to equation (1), when we substitute the value for atmospheric pressure, pressure by gas molecules and force by the piston, we get the following result:
$\Rightarrow mg + {P_{atmospheric}}A = {P_{gas}}A......\left( 2 \right)$
In the question we have given the following quantities,
$\Rightarrow g = 10\;{\text{m/}}{{\text{s}}^{\text{2}}}$
$\Rightarrow A = 4.0 \times {10^{ - 4}}\;{{\text{m}}^2}$
$\Rightarrow {P_{gas}} = 1.5 \times {10^5}\;{\text{Pa}}$
$\Rightarrow {P_{atmospheric}} = 1.0 \times {10^5}\;{\text{Pa}}$
Substituting the above values in equation (2), we get the following result:
$m \times 10 + \left( {1.5 \times {{10}^5} \times 4.0 \times {{10}^{ - 4}}} \right) = 1.0 \times {10^5} \times 4.0 \times {10^{ - 4}}$
Simplify the above expression we get,
$m \times 10 = 0.5 \times 4.0 \times 10$
After simplification we get
$m = 2\;{\text{kg}}$
So, after solving the above equation we get the value of mass of the piston which is $2\;{\text{kg}}$.

So, the correct option is option (B).

Note: As we know that the pressure applied by the piston and atmosphere is added. It is equal to the pressure applied by the gas molecules inside the cylinder. This is because the piston is not moving and so the force or the pressure is equal from both the sides, that is, above and below the piston.