Question

The gate of a canal is 8m wide. The level of water on one side is 30m and on the other side is 15m. The resultant force on the gate is –

& \text{A) 270}\times \text{1}{{\text{0}}^{5}}N \\\ & \text{B) 270}\times \text{1}{{\text{0}}^{6}}N \\\ & \text{C) 540}\times {{10}^{5}}N \\\ & \text{D) 540}\times \text{1}{{\text{0}}^{6}}N \\\ \end{aligned}$$

Answer 1

We need to carefully analyse the situation here. The gate has water on both sides of it at different heights. We can find the Force using Pascal's law of pressure distribution over an area. We should consider the mean pressure on both the sides.

Complete step by step answer:
We are given a canal system closed by a gate with water on both the sides. The water on each side is at different heights, which produces a resultant force on the gate without cancelling off.

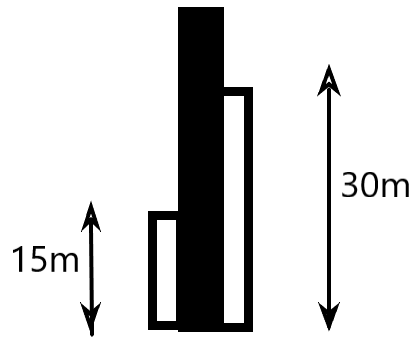
The gate has pressure exerted by the water on it due to the gauge pressure. The mean pressure exerted by the water on the gates has to be considered as the pressure is acted upon the same gate from the two sides.
${{P}_{m}}=\dfrac{\rho gh}{2}$
We can calculate the pressure on each side of the gate as –
${{P}_{1}}=\dfrac{\rho g{{h}_{1}}}{2}$
Given the height of the first side as 30m. So, we can get the pressure due to this as –
${{P}_{1}}=\dfrac{30\rho g}{2}$

The force exerted can be found using the Pascal’s law as –

& F=P\times A \\\ & \Rightarrow {{F}_{1}}={{P}_{1}}\times {{A}_{1}} \\\ & \Rightarrow {{F}_{1}}=\dfrac{30\rho g}{2}\times [(30\times 8)] \\\ & \Rightarrow {{F}_{1}}=\dfrac{30.1000.10.240}{2} \\\ & \therefore {{F}_{1}}=360\times {{10}^{6}}N \\\ \end{aligned}$$ Now, the pressure due to the second side of 15m high water as – $$\begin{aligned} & {{P}_{2}}=\dfrac{\rho g{{h}_{2}}}{2} \\\ & {{P}_{2}}=\dfrac{15\rho g}{2} \\\ \end{aligned}$$ Now, we can find the force due to this pressure using the Pascal’s law as – $$\begin{aligned} & F=P\times A \\\ & \Rightarrow {{F}_{2}}={{P}_{2}}\times {{A}_{2}} \\\ & \Rightarrow {{F}_{2}}=\dfrac{15\rho g}{2}\times [(15\times 8)] \\\ & \Rightarrow {{F}_{2}}=\dfrac{15.1000.10.120}{2} \\\ & \therefore {{F}_{2}}=90\times {{10}^{6}}N \\\ \end{aligned}$$ Now, we can calculate the net force as – $$\begin{aligned} & {{F}_{1}}-{{F}_{2}}=360\times {{10}^{6}}N-90\times {{10}^{6}}N \\\ & \therefore {{F}_{net}}=270\times {{10}^{6}}N \\\ \end{aligned}$$ The net force acting on the gate is $$270\times {{10}^{6}}N$$. **The correct answer is option B.** **Note:** The pressure distribution by Pascal's law is applicable for liquids only. If we were given two solid masses resting on the gate, we would have just calculated their force components due to each mass on either side to find the force acting on the gate.