Solveeit Logo
Login

Question

Question: The gas \({{A}_{2}}\) in the left flask allowed to react with gas \({{B}_{2}}\) present in right fla...

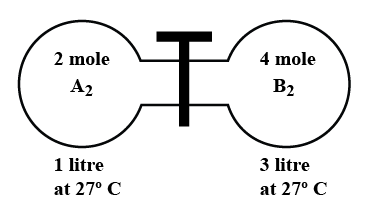
The gas A2{{A}_{2}} in the left flask allowed to react with gas B2{{B}_{2}} present in right flask at
A2(g)+B2(g)⇌2AB(g), Kc=4{{A}_{2}}(g)+{{B}_{2}}(g)\rightleftharpoons 2AB(g),\text{ }{{\text{K}}_{c}}=4 at 27∘C{{27}^{\circ }}C
What is the concentration of AB when equilibrium is established?

(a)- 1.33 M
(b)- 0.66 M
(c)- 0.33 M
(d)- 2.66 M

Explanation

Solution

We can solve this by using the formula Kc=[AB]2[A2][B2]{{K}_{c}}=\dfrac{{{[AB]}^{2}}}{[{{A}_{2}}][{{B}_{2}}]}. Given the volume is 1 liter of A2{{A}_{2}} and 3 liters of B2{{B}_{2}}, so the total volume of the system will be 3 + 1 = 4 liters.

Complete step-by-step answer: We are given the reaction as:
A2(g)+B2(g)⇌2AB(g){{A}_{2}}(g)+{{B}_{2}}(g)\rightleftharpoons 2AB(g)
1 mole of A2{{A}_{2}} reacts with 1 mole of B2{{B}_{2}} will produce 2 moles of AB. Given, the value of equilibrium constant isKc=4{{K}_{c}}=4. The Kc{{K}_{c}} means the value of the compounds are taken in concentrations.
In the diagram given above, there are 2 moles of A2{{A}_{2}} and 4 moles of B2{{B}_{2}}. Initially, the moles of A are 2, moles of B are 4, and mole of AB is 0. After time t, the moles of A will be 2-x, the moles of B will be 4-x, and the moles of AB will be 2x.
Given the volume is 1 liter of A2{{A}_{2}} and 3 liters of B2{{B}_{2}}, so the total volume of the system will be 3 + 1 = 4 liters.
We have to use the formula:
Kc=[AB]2[A2][B2]{{K}_{c}}=\dfrac{{{[AB]}^{2}}}{[{{A}_{2}}][{{B}_{2}}]}
The concentration of [AB] will be:
2x4=x2\dfrac{2x}{4}=\dfrac{x}{2}
The concentration of [B2][{{B}_{2}}] will be:
4−x4\dfrac{4-x}{4}
The concentration of [A2][{{A}_{2}}] will be:
2−x4\dfrac{2-x}{4}
Putting these values in the formula, will be:

Kc=[x2]2[2−x4][4−x4]{{K}_{c}}=\dfrac{{{\left[ \dfrac{x}{2} \right]}^{2}}}{\left[ \dfrac{2-x}{4} \right]\left[ \dfrac{4-x}{4} \right]}

4=4x2(4−x)(2−x)4=\dfrac{4{{x}^{2}}}{(4-x)(2-x)}
x2=(4−x)(2−x){{x}^{2}}=(4-x)(2-x)
Now, solving the equation will be:
x2=x2−6x+8{{x}^{2}}={{x}^{2}}-6x+8
6x = 8
The value of x will be:
x=43x=\dfrac{4}{3}
The concentration of AB is x2\dfrac{x}{2}, putting the value of x:
[AB]=23=0.66M[AB]=\dfrac{2}{3}=0.66M

Therefore, the correct answer is an option (b)- 0.66M.

Note: While writing the value of the equilibrium constant, then you have to take the concentration value only in which the number of moles of the compound must be divided with the total volume of the system.