Solveeit Logo
Login

Question

Question: The gap between the plates of a plates of a plate capacitor if filled with an isotropic insulator wh...

The gap between the plates of a plates of a plate capacitor if filled with an isotropic insulator whose di-electric constant varies in the direction perpendicular to the plates according to the law K=K1[1+sin⁡π4X]K={{K}_{1}}\left[ 1+\sin \dfrac{\pi }{4}X \right], where d is the separation, between the plates and K1{{K}_{1}} is a constant. The area of the plates is S. Determine the capacitance of the capacitor.

Explanation

Solution

Hint We should know that capacitance is the ratio of the change in electric charge of a system to the corresponding change in its electrical potential. There are two closely related notions of the capacitance, which are self-capacitance and mutual capacitance. Any object that can be electrically charged always exhibits the property of self-capacitance. Based on this concept we have to solve the question.

Complete step by step answer
Let us consider a small element dx width at a distance x from P and let us calculate the small capacitor:
Here is the diagram that is given below:

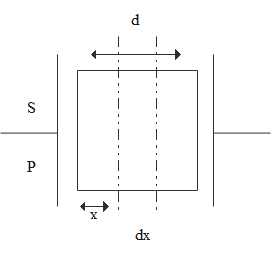
The main formula is given as:
(dc)=ε0K(S)dx(dc)=\dfrac{{{\varepsilon }_{0}}K(S)}{dx}
So, now we have to evaluate the expression as:
dc=ε0K1[1+sin⁡πdx]dxdc=\dfrac{{{\varepsilon }_{0}}{{K}_{1}}[1+\sin \dfrac{\pi }{d}x]}{dx}
Now we have to integrate the above expression:
∫1dc=1ceff=∫0ddxε0K1[1+sin⁡πdx](S)\int{\dfrac{1}{dc}}=\dfrac{1}{ceff}=\int{_{0}^{d}}\dfrac{dx}{{{\varepsilon }_{0}}{{K}_{1}}[1+\sin \dfrac{\pi }{d}x](S)}
So, after the evaluation we get that:
=1Sε0K1∫0ddx1+sin⁡πdx×1−sin⁡πdx1−sin⁡πdx=\dfrac{1}{S{{\varepsilon }_{0}}{{K}_{1}}}\int{_{0}^{d}}\dfrac{dx}{1+\sin \dfrac{\pi }{d}x}\times \dfrac{1-\sin \dfrac{\pi }{d}x}{1-\sin \dfrac{\pi }{d}x}
=1Sε0K1∫0d1−sin⁡πd×(dx)1−sin⁡2πdx=\dfrac{1}{S{{\varepsilon }_{0}}{{K}_{1}}}\int{_{0}^{d}}\dfrac{1-\sin \dfrac{\pi }{d}\times (dx)}{1-{{\sin }^{2}}\dfrac{\pi }{d}x}
=2dSε0K1π=1ceff=\dfrac{2d}{S{{\varepsilon }_{0}}{{K}_{1}}\pi }=\dfrac{1}{ceff}
Now on the further evaluation we get:
=1Sε0K1[∫0dsec⁡2πd×dx−∫0dsec⁡×πdtan⁡πd×dx]=\dfrac{1}{S{{\varepsilon }_{0}}{{K}_{1}}}[\int{_{0}^{d}{{\sec }^{2}}\dfrac{\pi }{d}\times dx-\int{_{0}^{d}\sec \times \dfrac{\pi }{d}}}\tan \dfrac{\pi }{d}\times dx]
=1Sε0K1[[dπtan⁡πdx]0d−[dπsec⁡πdx]0d]=\dfrac{1}{S{{\varepsilon }_{0}}{{K}_{1}}}\left[ \left[ \dfrac{d}{\pi }\tan \dfrac{\pi }{d}x \right]_{0}^{d}-\left[ \dfrac{d}{\pi }\sec \dfrac{\pi }{d}x \right]_{0}^{d} \right]
=2dSε0K1π=1ceff=\dfrac{2d}{S{{\varepsilon }_{0}}{{K}_{1}}\pi }=\dfrac{1}{ceff}
So, we get that:
ceff=Sε0πK12dceff=\dfrac{S{{\varepsilon }_{0}}\pi {{K}_{1}}}{2d}
Hence, we can say that the capacitance of the capacitor is given as: ceff=Sε0πK12dceff=\dfrac{S{{\varepsilon }_{0}}\pi {{K}_{1}}}{2d}

Note We should know that self-capacitance is defined as the coupling of one plate capacitor to the virtual ground. This change in the self- capacitance can be determined by us as the distance to the finger. Self-capacitance is often used in the button, slider or in some cases we can use the wheel sensors which are also known as BSW.
Now let us define the concept of mutual capacitance. When we say mutual capacitance, which is denoted by C we mean that between any two conductors, let Q be the charge that is stored on each of the plates, V be the per unit voltage difference between the plates.
The main classical calculation of the capacitance is given by us in the form of Gauss’s and Poisson’s equation for any given system.