Question

The gap between any two rails, each of length $l$ laid on a railway track equals $x$ at ${27^{\text{o}}}{\text{C}}$. When the temperature rises to ${40^{\text{o}}}{\text{C}}$, the gap closes up. The coefficient of linear expansion of the material of the rail is $\alpha$. The length of a rail at ${27^{\text{o}}}{\text{C}}$ will be

A. $\dfrac{x}{{26\alpha }}$
B. $\dfrac{x}{{13\alpha }}$
C. $\dfrac{{2x}}{{13\alpha }}$
D. None of these

Answer 1

It is a question of linear expansion and here you will need to use the formula of linear expansion. To use this formula, you will need to find out the increase in length when the temperature rises to ${40^{\text{o}}}{\text{C}}$. It is given that the gap closes up, use this information to find the increased length. Then use this increased length to get the value of the length at initial temperature.

Complete step by step answer:
Given, the length of each rail is $l$ at temperature $T = {27^{\text{o}}}{\text{C}}$.
Gap between two rails is $x$ at temperature $T = {27^{\text{o}}}{\text{C}}$.
Coefficient of linear expansion of the material of the rail is $\alpha$.

Let the length of a rail be temperature $T' = {40^{\text{o}}}{\text{C}}$ be $l'$.We will use the formula of linear expansion, which is
${\alpha _L} = \dfrac{1}{L}\dfrac{{dL}}{{dT}}$ (i)
where ${\alpha _L}$ is coefficient of linear expansion, $L$ is the original length, $dT$ is the change in temperature and $dL$ is the change in length.
In the question it is said that when the temperature rises to $T' = {40^{\text{o}}}{\text{C}}$, the gap closes up that is the length of the rails increases such that the gap vanishes. Since, the rails are of same material and their coefficient of linear expansion is same so the increase in length will be same which means the initial gap $x$ will get divided equally in increase in length of the rails.
Let us understand with the diagram of two rails.

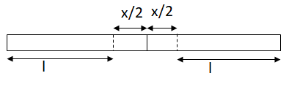
So, the length after temperature rises to $T' = {40^{\text{o}}}{\text{C}}$ will be,
$l' = l + \dfrac{x}{2}$
Here, the original length is $l$ and length after temperature is $l'$
So, the change in length will be, $dl = l' - l$
Change in temperature will be, $dT = T' - T$
Therefore, using the formula of linear expansion from equation (i), we get
$\alpha = \dfrac{1}{l}\dfrac{{dl}}{{dT}}$
Putting the values of $dl$ and $dT$ in the above equation, we get
$\alpha = \dfrac{1}{l}\dfrac{{\left( {l' - l} \right)}}{{\left( {T' - T} \right)}}$
Putting the values of $l'$, $T'$ and $T$, we get
$\alpha = \dfrac{1}{l}\dfrac{{\left( {l + \dfrac{x}{2} - l} \right)}}{{\left( {40 - 27} \right)}}$
$\Rightarrow \alpha = \dfrac{1}{l}\dfrac{{\left( {\dfrac{x}{2}} \right)}}{{\left( {13} \right)}}$
$\Rightarrow \alpha = \dfrac{x}{{26l}}$
$\therefore l = \dfrac{x}{{26\alpha }}$
Therefore, the length of the rail at ${27^{\text{o}}}{\text{C}}$ is $\dfrac{x}{{26\alpha }}$.

Hence, the correct answer is option A.

Note: There are three types of thermal expansion. The first is linear expansion, which we have discussed in the above question. The second is area expansion, which is an increase in area of a substance due to rise in temperature. The third is volume expansion, which is an increase in volume of a substance due to rise in temperature.