Question

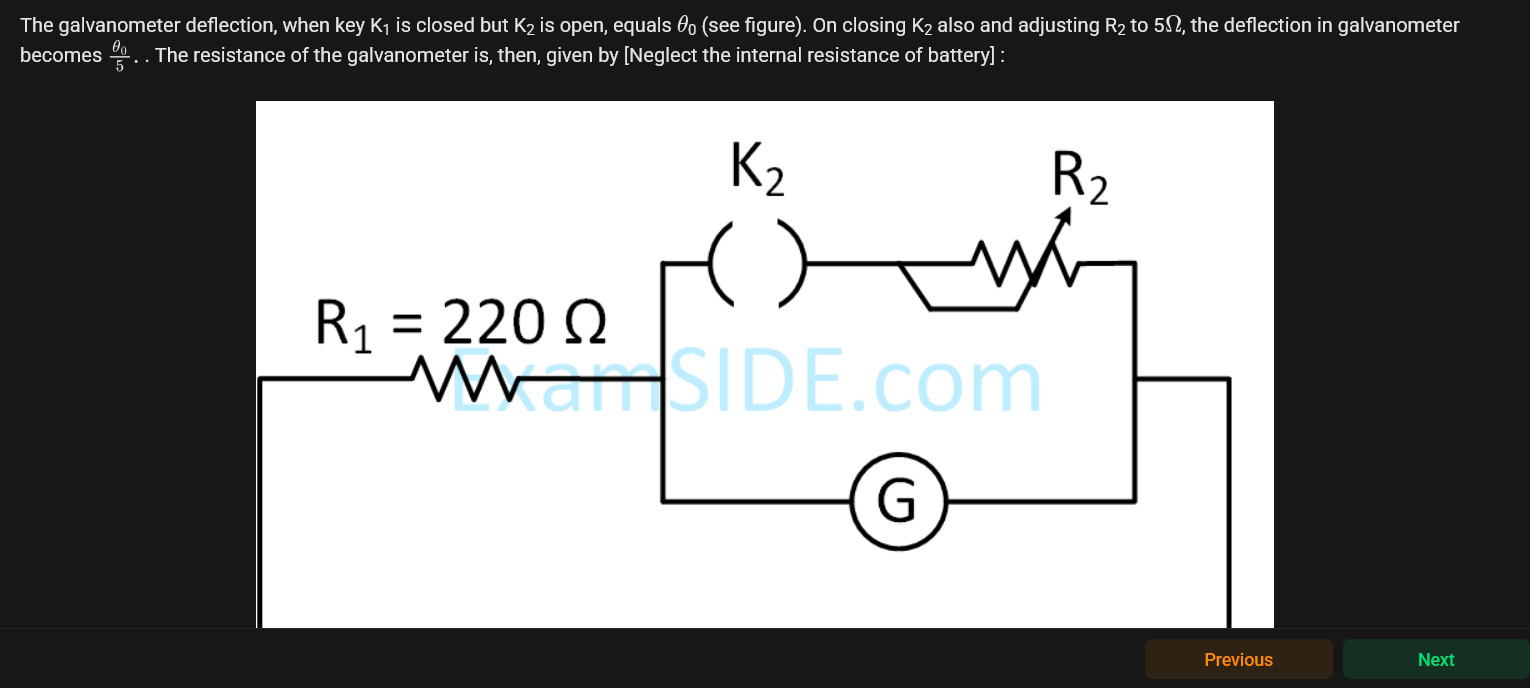
The galvanometer deflection, when key K₁ is closed but K2 is open, equals $\theta_0$ (see figure). On closing K2 also and adjusting R2 to 5$\Omega$, the deflection in galvanometer becomes $\frac{\theta_0}{5}$. The resistance of the galvanometer is, then, given by [Neglect the internal resistance of battery] :

• A. 22 $\Omega$
• B. 20 $\Omega$
• C. 25 $\Omega$
• D. 110 $\Omega$

Answer 1

Answer: (A)

22 $\Omega$

Answer 2

Let $V$ be the battery voltage and $R_G$ be the galvanometer resistance. When K₁ is closed and K₂ is open, the current through the galvanometer is $I_{G1} \propto \theta_0$. When K₂ is also closed and $R_2 = 5\Omega$, the galvanometer current is $I_{G2} \propto \frac{\theta_0}{5}$. We have $I_{G1} = \frac{V}{R_1 + R_G}$ and $I_{G2} = \frac{V R_2}{R_1(R_G+R_2) + R_G R_2}$. Given $I_{G2} = \frac{1}{5} I_{G1}$, we get $R_G = \frac{4 R_1 R_2}{R_1 - 4 R_2}$. Substituting $R_1 = 220\Omega$ and $R_2 = 5\Omega$, $R_G = \frac{4 \times 220 \times 5}{220 - 4 \times 5} = \frac{4400}{200} = 22\Omega$.