Question

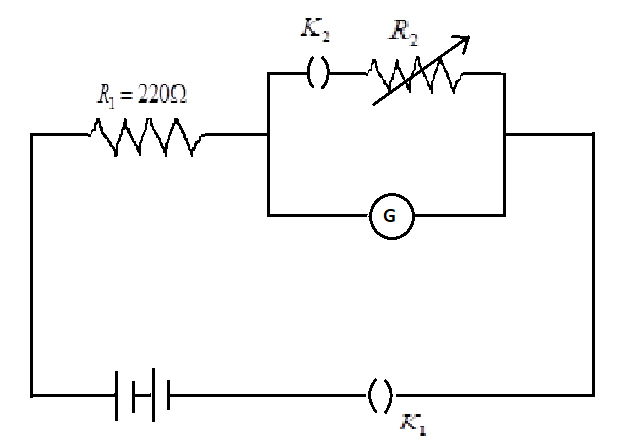
The galvanometer deflection, when key $K_1$ is closed but $K_2$ is open, equals ${\theta _0}$ (see figure). On closing $K_2$ also and adjusting $R_2$ to $5\Omega$, the deflection in the galvanometer becomes $\dfrac{{{\theta _0}}}{5}$. The resistance of the galvanometer is, then, given by: [Neglect the internal resistance of battery]:

A) $12\Omega$
B) $25\Omega$
C) $5\Omega$
D) $22\Omega$

Answer 1

In this question, you have asked for the resistance for the galvanometer and given the two conditions. Firstly make the circuit according to the two conditions given and then form the two equations. Then after solving two equations you will get the resistance of the galvanometer.

Complete step by step solution:
Case 1: In the first case, it is given that, when the key $K_1$ is closed but $K_2$ is open then deflection in the galvanometer equals ${\theta _0}$.
Let the current flowing in the galvanometer is ${i_g}$ and the deflection in the galvanometer is given by ${\theta _0}$. We know that the current in the galvanometer is proportional to the deflection in the galvanometer.
Thus, ${i_g} \propto {\theta _0}$
After removing proportional sign we get a constant C,
${i_g} = C{\theta _0}$ …….(i)
Let us assume the emf of the battery is $E$.
We know that the current flowing in the circuit is equal to the ratio of emf of the battery to the total resistance in the circuit.
So, ${i_g} = \dfrac{E}{{220 + {R_g}}}$ ……..(ii)
From equation (i) and (ii), we get
$\dfrac{E}{{220 + {R_g}}} = C{\theta _0}$ ………..(iii)

Case 2:
Now, according to the second condition when $K_2$ is closed and adjusting $R_2$ to $5\Omega$, the deflection in the galvanometer becomes $\dfrac{{{\theta _0}}}{5}$.
We know that the current in the galvanometer is proportional to the deflection in the galvanometer. Here deflection is $\dfrac{{{\theta _0}}}{5}$.
${i_g} = C\dfrac{{{\theta _0}}}{5}$ …….(iv)
We know that the current flowing in the circuit is equal to the ratio of emf of the battery to the total resistance in the circuit.
${i_g} = \left( {\dfrac{E}{{220 + \dfrac{{5{R_g}}}{{5 + {R_g}}}}}} \right) \times \left( {\dfrac{5}{{{R_g} + 5}}} \right)$ …….(v)
From equation (iv) and (v), we get
$\left( {\dfrac{E}{{220 + \dfrac{{5{R_g}}}{{5 + {R_g}}}}}} \right) \times \left( {\dfrac{5}{{{R_g} + 5}}} \right) = C\dfrac{{{\theta _0}}}{5}$
On further solving this, we get
$\Rightarrow \dfrac{{5E}}{{225{R_g} + 1100}} = \dfrac{{C{\theta _0}}}{5}$ ……..(vi)
Now finally solving equation (iii) and (vi) from case 1 and 2 respectively, we get,
$\Rightarrow \dfrac{{225{R_g} + 1100}}{{1100 + 5{R_g}}} = 5$
On further solving, we get
$\Rightarrow 5500 + 25{R_g} = 225{R_g} + 1100$
$\Rightarrow 200{R_g} = 4400$
On finally solving this, we get
${R_g} = 22\Omega$
Thus, the resistance of the galvanometer is $22\Omega$.

Therefore, the correct answer is (D), $22\Omega$.

Note: Always keep in mind the circuit given and apply the conditions accordingly. Always mention the SI units of each and every term used and also keep in mind the direction of the current while solving these types of circuit questions. A galvanometer is an electromechanical instrument used for detecting and indicating electric current. A galvanometer works as an actuator, by producing a rotary deflection, in response to electric current flowing through a coil in a constant magnetic field.