Question

The fundamental frequency of a closed pipe is $220{\text{ }}Hz$. If ${\left( {\dfrac{1}{4}} \right)^{th}}$ of the pipe is filled with water. The frequency of the 1st overtone of the pipe now is
a. $220Hz$
b. $440Hz$
c. $880Hz$
d. $1760Hz$

Answer 1

Find the formula for the frequency of the fundamental tone in a closed pipe for a certain length.
Note that there are many overtones exit in that pipe. Find the first overtone that is three times the fundamental tone. The next tone of the fundamental tone is called the first, the first overtone.
In this problem, it is given that the length decreases to a certain amount after filling the pipe with water. So use the value of decreased length for calculating the first overtone.

Formula used:
The fundamental tone of the closed pipe in the frequency, ${\upsilon _0} = \dfrac{V}{{4l}}$
$V$ is the velocity of the sound.
$l$ is the length of the pipe.
The frequency of the first overtone, ${\upsilon _1} = 3{\upsilon _0}$

Complete step by step answer:
The antinode of the simplest stationary wave that is created in the closed pipe is situated at the closed side and the node is situated at the open side of the closed pipe. Hence in the middle of the pipe there is no node or antinode (fig-1). So, the tone created in the pipe is called the fundamental tone.

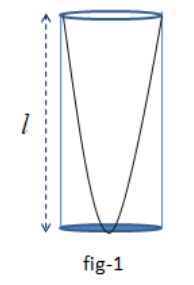
If the wavelength is ${\lambda _0}$ ,
The length of the pipe, $l =$ the distance between the consequent antinode and node = $\dfrac{{{\lambda _0}}}{4}$
So, ${\lambda _0} = 4l$
Hence, the the frequency of the tone, ${\upsilon _0} = \dfrac{V}{{{\lambda _0}}} = \dfrac{V}{{4l}}$, this tone is the fundamental tone.

When another pair of antinodes and nodes exist in the middle of the pipe, the next tone occurs. This is the first overtone.
The frequency of the first overtone, ${\upsilon _1} = 3{\upsilon _0}$
When we have ${\left( {\dfrac{1}{4}} \right)^{th}}$ of the pipe is filled with water, and also the length of the pipe decreases to ${\left( {\dfrac{3}{4}} \right)^{th}}$ to its length.
So now the length will be $\dfrac{{3l}}{4}$.

So, the frequency of the overtone will be, ${\upsilon _1} = 3{\upsilon _0} = \dfrac{{3V}}{{4\left( {\dfrac{{3l}}{4}} \right)}}$
${\upsilon _1} = \dfrac{V}{l}$

Now, ${\upsilon _0} = \dfrac{V}{{4l}}$
$\Rightarrow \dfrac{V}{l} = 4{\upsilon _0}$
$\Rightarrow {\upsilon _1} = 4{\upsilon _0}$
Given the fundamental tone, ${\upsilon _0} = 220Hz$
$\therefore {\upsilon _1} = 4 \times 220 = 880Hz$.

Hence, the correct answer is option (C).

Note: When there is another pair of antinode and node exists between the antinode of closed side and node of the open side of the closed pipe, then the next tone after the fundamental tone occurs. This is the first overtone (fig-2).

Here the wavelength is ${\lambda _1}$ ,
The length of the pipe, $l =$ the distance between the antinode of closed side and the next second node = $\dfrac{{3{\lambda _1}}}{4}$
So, ${\lambda _0} = \dfrac{{4l}}{3}$
Hence, the the frequency of the tone, ${\upsilon _1} = \dfrac{V}{{{\lambda _1}}} = \dfrac{{3V}}{{4l}} = 3{\upsilon _0}$.