Question

The function y = a(1 - cos x) is maximum when x =

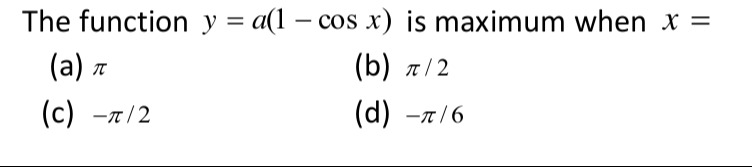
• A. π
• B. π/2
• C. -π/2
• D. -π/6

Answer 1

Answer: (A)

π

Answer 2

The function given is $y = a(1 - \cos x)$. To find the maximum, we analyze the term $(1 - \cos x)$.

The range of $\cos x$ is $[-1, 1]$. Therefore, the range of $-\cos x$ is $[-1, 1]$. Adding 1, the range of $(1 - \cos x)$ is $[0, 2]$.

The maximum value of $(1 - \cos x)$ is 2, which occurs when $\cos x = -1$. The values of $x$ for which $\cos x = -1$ are $x = (2n + 1)\pi$, where $n$ is an integer.

Assuming $a > 0$, the function is maximum when $\cos x = -1$, i.e., $x = (2n + 1)\pi$.

Checking the options:

• x = π. cos(π) = -1. y = a(1 - (-1)) = 2a
• x = π/2. cos(π/2) = 0. y = a(1 - 0) = a
• x = -π/2. cos(-π/2) = 0. y = a(1 - 0) = a
• x = -π/6. cos(-π/6) = √3/2. y = a(1 - √3/2)

Therefore, the function $y = a(1 - \cos x)$ is maximum when $x = \pi$.