Question

The function which is neither decreasing nor increasing in $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$ is
A) $\text{cosec }x$
B) $\tan x$
C) ${{x}^{2}}$
D) $\left| x-1 \right|$

Answer 1

In this type of question we have to use the concept of increasing and decreasing function. We know that a function $f\left( x \right)$ is said to be an increasing function if $f'\left( x \right)>0$ while a function $f\left( x \right)$ is said to be an decreasing function if $f'\left( x \right)<0$. Here, we consider each of the functions separately and check whether the function is increasing or decreasing. The function which does not satisfy both conditions in the given interval is our required result.

Complete step by step answer:
Now we have to find the function which is neither decreasing nor increasing in $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$
Let us consider the function
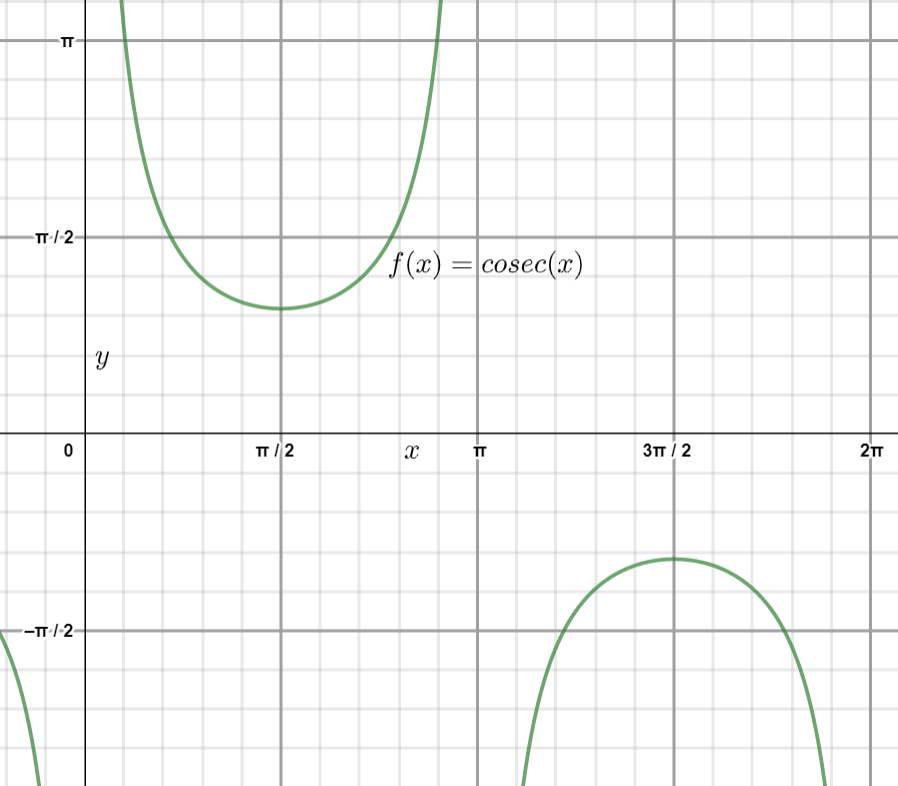
$\Rightarrow f\left( x \right)=\text{cosec }x$
By differentiating with respect to $x$ we get,
$\Rightarrow f'\left( x \right)=-\text{cosec }x\cot x$
We know that in the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$ at $x=\pi$, $\text{cosec }x$ and $\cot x$ both are undefined
Hence, we can say that the function $f'\left( x \right)=-\text{cosec }x\cot x$ is undefined.
Thus, the function $f\left( x \right)=\text{cosec }x$ is neither decreasing or increasing in the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$
Now, let us consider
$\Rightarrow f\left( x \right)=\tan x$
By differentiating with respect to $x$ we get,
$\Rightarrow f'\left( x \right)={{\sec }^{2}}x$
As we know that ${{\sec }^{2}}x$ is a square obviously $f'\left( x \right)>0$ and hence we say that the function $f\left( x \right)=\tan x$ is an increasing function in $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$
Now we consider the third function
$\Rightarrow f\left( x \right)={{x}^{2}}$
By differentiating with respect to $x$ we get,
$\Rightarrow f'\left( x \right)=2x$
Now in the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$ we observe that all the values of $x$ are positive
$\Rightarrow f'\left( x \right)=2x>0$
Hence, we can say that the function $f\left( x \right)={{x}^{2}}$ is an increasing function in the given interval
And now let us consider the last function
$\Rightarrow f\left( x \right)=\left| x-1 \right|$
By differentiating with respect to $x$ we get,
$\Rightarrow f'\left( x \right)=c$ where $c$ is a constant which may be positive or negative.
So we say that if $c$ is positive then the function is increasing and if $c$ is negative then the function is decreasing.
Hence, we get the function $f\left( x \right)=\left| x-1 \right|$ which is either increasing or decreasing in the given interval.
Thus we have the function $f\left( x \right)=\text{cosec }x$ which is neither decreasing nor increasing in the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$.
So, the correct answer is Option (A).

Note: In this type of question students have to note the definition of the increasing and decreasing functions. Students have to remember the values of some trigonometric functions such as$\text{cosec }\pi ,\cot \pi$, if not then at least the values of $\sin \pi ,\cos \pi$ so that they can identify the required values. Also from the nature of the graph of the function $f\left( x \right)=\text{cosec }x$ students can easily identify that the function is neither increasing nor decreasing in the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$