Question

The function $f(x) = ||e^x -1| -1|$ is:

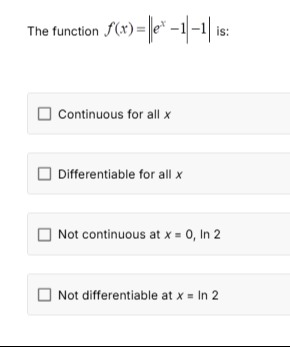
• A. Continuous for all $x$
• B. Differentiable for all $x$
• C. Not continuous at $x = 0, \ln 2$
• D. Not differentiable at $x = \ln 2$

Answer 1

Answer: (A), (D)

Continuous for all x, Not differentiable at x = ln 2

Answer 2

To analyze the function $f(x) = ||e^x -1| -1|$, we will examine its continuity and differentiability by breaking it down into simpler components and considering the points where the arguments of the absolute value functions become zero.

Let's define the function piecewise.

Step 1: Analyze $g(x) = e^x - 1$.

The critical point for the inner absolute value is when $e^x - 1 = 0$, which implies $e^x = 1$, so $x = 0$.

Step 2: Analyze $h(x) = |e^x - 1|$.

$h(x) = \begin{cases} e^x - 1 & \text{if } e^x - 1 \ge 0 \implies x \ge 0 \\ -(e^x - 1) & \text{if } e^x - 1 < 0 \implies x < 0 \end{cases}$

$h(x) = \begin{cases} e^x - 1 & \text{if } x \ge 0 \\ 1 - e^x & \text{if } x < 0 \end{cases}$

Step 3: Analyze $k(x) = |e^x - 1| - 1$.

$k(x) = \begin{cases} (e^x - 1) - 1 & \text{if } x \ge 0 \\ (1 - e^x) - 1 & \text{if } x < 0 \end{cases}$

$k(x) = \begin{cases} e^x - 2 & \text{if } x \ge 0 \\ -e^x & \text{if } x < 0 \end{cases}$

The critical points for the outer absolute value are when $k(x) = 0$.

For $x \ge 0$: $e^x - 2 = 0 \implies e^x = 2 \implies x = \ln 2$. (Note: $\ln 2 \approx 0.693$, which is $\ge 0$).

For $x < 0$: $-e^x = 0$, which has no solution.

So, $x = \ln 2$ is a critical point for the outer absolute value.

Step 4: Analyze $f(x) = ||e^x - 1| - 1| = |k(x)|$.

We need to consider the sign of $k(x)$ in different intervals.

• For $x < 0$: $k(x) = -e^x$. Since $e^x > 0$ for all $x$, $-e^x < 0$. So, $f(x) = |-e^x| = e^x$ for $x < 0$.
• For $x \ge 0$: $k(x) = e^x - 2$.
  • If $e^x - 2 \ge 0 \implies x \ge \ln 2$: $f(x) = e^x - 2$.
  • If $e^x - 2 < 0 \implies x < \ln 2$: $f(x) = -(e^x - 2) = 2 - e^x$.

Combining these, the piecewise definition of $f(x)$ is:

$f(x) = \begin{cases} e^x & \text{if } x < 0 \\ 2 - e^x & \text{if } 0 \le x < \ln 2 \\ e^x - 2 & \text{if } x \ge \ln 2 \end{cases}$

Continuity Analysis:

1. Continuity within intervals: Each piece ($e^x$, $2-e^x$, $e^x-2$) is an exponential or linear function, which are continuous on their respective intervals.

2. Continuity at boundary points:

   • At $x = 0$:

     $f(0^-) = \lim_{x \to 0^-} e^x = e^0 = 1$.

     $f(0^+) = \lim_{x \to 0^+} (2 - e^x) = 2 - e^0 = 2 - 1 = 1$.

     $f(0) = 2 - e^0 = 1$.

     Since $f(0^-) = f(0^+) = f(0)$, $f(x)$ is continuous at $x=0$.

   • At $x = \ln 2$:

     $f(\ln 2^-) = \lim_{x \to \ln 2^-} (2 - e^x) = 2 - e^{\ln 2} = 2 - 2 = 0$.

     $f(\ln 2^+) = \lim_{x \to \ln 2^+} (e^x - 2) = e^{\ln 2} - 2 = 2 - 2 = 0$.

     $f(\ln 2) = e^{\ln 2} - 2 = 0$.

     Since $f(\ln 2^-) = f(\ln 2^+) = f(\ln 2)$, $f(x)$ is continuous at $x=\ln 2$.

Since $f(x)$ is continuous on all intervals and at the boundary points, it is continuous for all $x \in \mathbb{R}$.

Therefore, the statement "Continuous for all $x$" is correct. The statement "Not continuous at $x = 0, \ln 2$" is incorrect.

Differentiability Analysis:

We need to check differentiability at the boundary points $x=0$ and $x=\ln 2$.

First, let's find the derivative of each piece:

$f'(x) = \begin{cases} e^x & \text{if } x < 0 \\ -e^x & \text{if } 0 < x < \ln 2 \\ e^x & \text{if } x > \ln 2 \end{cases}$

1. At $x = 0$:

   Left-hand derivative: $f'(0^-) = \lim_{x \to 0^-} e^x = e^0 = 1$.

   Right-hand derivative: $f'(0^+) = \lim_{x \to 0^+} (-e^x) = -e^0 = -1$.

   Since $f'(0^-) \neq f'(0^+)$, $f(x)$ is not differentiable at $x=0$.

2. At $x = \ln 2$:

   Left-hand derivative: $f'(\ln 2^-) = \lim_{x \to \ln 2^-} (-e^x) = -e^{\ln 2} = -2$.

   Right-hand derivative: $f'(\ln 2^+) = \lim_{x \to \ln 2^+} (e^x) = e^{\ln 2} = 2$.

   Since $f'(\ln 2^-) \neq f'(\ln 2^+)$, $f(x)$ is not differentiable at $x=\ln 2$.

Therefore, the statement "Differentiable for all $x$" is incorrect. The statement "Not differentiable at $x = \ln 2$" is correct.

Conclusion:

The function $f(x) = ||e^x -1| -1|$ is:

1. Continuous for all $x$.
2. Not differentiable at $x = 0$ and $x = \ln 2$.