Question
Question: The function $f(x)=\cos^{-1}\left(\frac{2\lfloor |\sin x|+|\cos x| \rfloor}{\sin^2 x+2\sin x+\frac{1...
The function f(x)=cos−1(sin2x+2sinx+4112⌊∣sinx∣+∣cosx∣⌋) is defined if x belongs to: (where ⌊.⌋ represents the greatest integer function)
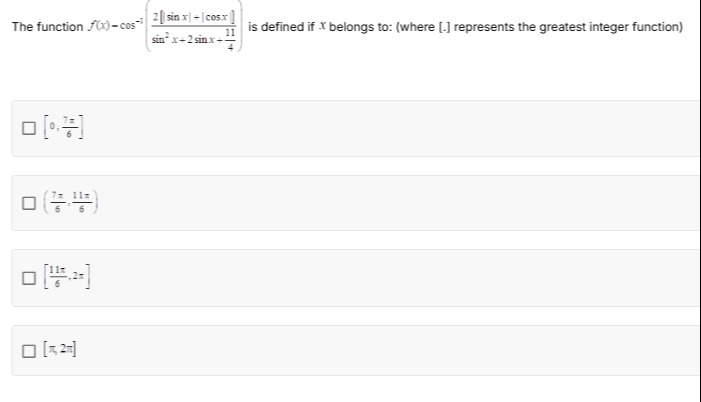
[0, \frac{7\pi}{6}]
(\frac{7\pi}{6}, \frac{11\pi}{6})
[\frac{11\pi}{6}, 2\pi]
[\pi, 2\pi]
[0, \frac{7\pi}{6}]
Solution
To find the domain of the function f(x)=cos−1(sin2x+2sinx+4112⌊∣sinx∣+∣cosx∣⌋), we need to ensure that the argument of the cos−1 function lies in the interval [−1,1].
Let the argument be Y=sin2x+2sinx+4112⌊∣sinx∣+∣cosx∣⌋.
Step 1: Analyze the Numerator
Let N=2⌊∣sinx∣+∣cosx∣⌋. We know that for any real x, 1≤∣sinx∣+∣cosx∣≤2. To prove this, let S=∣sinx∣+∣cosx∣. Then S2=(∣sinx∣+∣cosx∣)2=sin2x+cos2x+2∣sinxcosx∣=1+∣sin(2x)∣. Since 0≤∣sin(2x)∣≤1, we have 1≤S2≤2. Taking the square root, 1≤S≤2. Since 2≈1.414, we have 1≤∣sinx∣+∣cosx∣≤1.414. Therefore, the greatest integer less than or equal to ∣sinx∣+∣cosx∣ is ⌊∣sinx∣+∣cosx∣⌋=1. So, the numerator N=2×1=2.
Step 2: Analyze the Denominator
Let D=sin2x+2sinx+411. Let t=sinx. Since −1≤sinx≤1, we have −1≤t≤1. The denominator can be rewritten by completing the square: D=t2+2t+1+411−1=(t+1)2+47. Now, we find the range of D for t∈[−1,1]. The minimum value of (t+1)2 occurs at t=−1, where (t+1)2=(−1+1)2=0. The maximum value of (t+1)2 occurs at t=1, where (t+1)2=(1+1)2=22=4. So, 0≤(t+1)2≤4. Adding 47 to all parts of the inequality: 47≤(t+1)2+47≤4+47, which simplifies to 47≤D≤423. Note that D>0 for all x.
Step 3: Apply the condition for cos−1
The argument of cos−1 is Y=DN=D2. For cos−1(Y) to be defined, we must have −1≤Y≤1. Since D>0, Y=D2 will always be positive. So, Y>0. Therefore, we only need to satisfy the condition Y≤1, which means D2≤1. Since D>0, we can multiply by D without changing the inequality direction: 2≤D.
Step 4: Find the condition on sinx
Substitute the expression for D: (sinx+1)2+47≥2. This simplifies to (sinx+1)2≥41. Taking the square root of both sides: ∣sinx+1∣≥21. This inequality implies two cases:
Case 1: sinx+1≥21, which gives sinx≥−21.
Case 2: sinx+1≤−21, which gives sinx≤−23. Since the range of sinx is [−1,1], the condition sinx≤−23 is impossible.
Thus, the only condition for f(x) to be defined is sinx≥−21.
Step 5: Determine the interval for x
We need to find the values of x for which sinx≥−21. In the interval [0,2π], sinx=−21 at x=π+6π=67π and x=2π−6π=611π. The values of x for which sinx≥−21 are x∈[0,67π]∪[611π,2π] (and periodically).
Comparing with the options, [0,67π] is a subset of the domain.
