Question

The function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$
A. is a constant function
B. has a domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$
C. is such that $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$
D. is aperiodic

Answer 1

Hint: First try to simplify the given function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.Then proceeds to the options provided to verify one by one. Here, aperiodic means irregularity.

Complete step-by-step answer:
Here, we have a function given as$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}\ldots \ldots (1)$.
We need to find correct answer/answers by observing all the options given.
Now, Option A. is given as ${{x}^{\dfrac{1}{\ln x}}}$is a constant function.
We can verify this option by just simplifying the function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$given in the problem.
We have $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$
Taking log to both sides, we get
${{\log }_{e}}\left( f\left( x \right) \right)={{\log }_{e}}{{\left( x \right)}^{\dfrac{1}{\ln x}}}\ldots \ldots (2)$
We know property of log as
$\log {{m}^{n}}=n\log m$
So, we can write equation (2) as
${{\log }_{e}}\left( f\left( x \right) \right)=\dfrac{1}{\ln x}{{\log }_{e}}\left( x \right)$
Here ${{\log }_{e}}x$ has base ‘e’ and we know that $\ln x={{\log }_{e}}x$(same value with different representations).
${{\log }_{e}}\left( f\left( x \right) \right)=1$
Now, we know that if
${{\log }_{a}}N=x$, then
$N={{a}^{x}}$
Hence,${{\log }_{e}}\left( f\left( x \right) \right)=1$, can be written as
$\begin{aligned} & f\left( x \right)=e'=e \\\ & f\left( x \right)=e \\\ \end{aligned}$
Hence, given function f(x) is ‘e’ i.e. Constant function.
So, Option A is correct.
Now, Coming to option B. i.e. f(x) has a domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
To verify option ‘B’, we need to calculate the domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.
The given function is in volument of ‘$\ln x$’. So, we cannot put negative values to a given function f(x) because the domain of $\ln x$ is ${{R}^{+}}$or$\left( 0,\infty \right)$.
We know the value of ln1 is 0. So, $\dfrac{1}{\ln x}$cannot take x=1 as well because $\dfrac{1}{0}$is not defined.
Hence, domain of ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, option B. is not the correct answer.
Now, to verify option ‘C’ i.e. function $f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$ is such that $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$ exist,
We need to calculate LHL and RHL for x=1 i.e. $x\to {{1}^{-}}$and$x\to {{1}^{+}}$.
Now, we have already calculated that $f\left( x \right)=e$ for the domain$\left( 0,1 \right)\bigcup \left( e,\infty \right)$.
So, $\ln x$ LHL ($x\to {{1}^{-}}$) and RHL ($x\to {{1}^{+}}$).
We have constant function ‘e’. So the limit at $x\to 1$will exist.
So, option C. is the correct answer.
As ${{\left( x \right)}^{\dfrac{1}{\ln x}}}$ is simplified to ‘e’.
Hence graph of given function i.e.
$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$Is given as

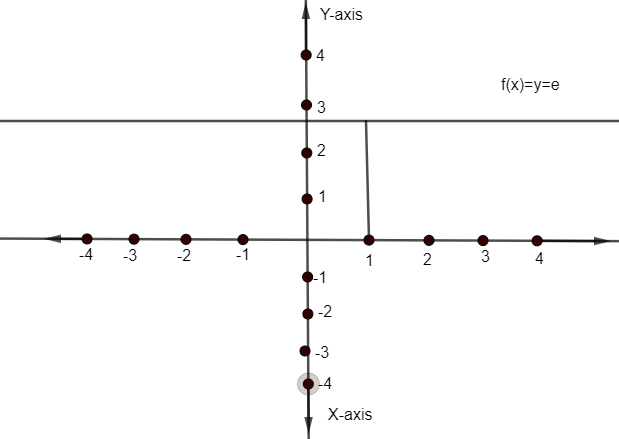
Hence, a given function is aperiodic as well where aperiodic means irregularity or not periodic function.
Hence option D. is also correct.

Note: One can go wrong if he/she will not simplify the given relation. As one can think that a given function is written in terms of ‘x’ so how it could be a constant function. So, be careful with these kinds of problems.
One can go wrong with the domain of${{\left( x \right)}^{\dfrac{1}{\ln x}}}$. As domain of ${{x}^{a}}$is ‘R’ i.e. All real numbers. So, one can get confused with it. So, checking domain for $\dfrac{1}{\ln x}$is the key point for calculation of domain of$f\left( x \right)={{x}^{\dfrac{1}{\ln x}}}$.