Question

The function $f$ is defined by

1 - x,x < 0 \\\ 1,x = 0 \\\ x + 1,x > 0 \\\ \right.$$ . Draw the graph of $$f(x)$$ .

Answer 1

A function is nothing but an expression which defines a relationship between the independent variable and the dependent variable. For instance, let us consider a function $f(x) = y$ , here $y$ is the dependent variable and $x$ is the independent variable. The variable $y$ will get a value for each value of $x$ .

Complete step by step answer:
It is given that f(x) = \left\\{ 1 - x,x < 0 \\\ 1,x = 0 \\\ x + 1,x > 0 \\\ \right.
that is,
When $x < 0$ , $f(x) = 1 - x$
When $x = 0$ , $f(x) = 1$
When $x > 0$ , $f(x) = x + 1$
First, we have to find the points from the given function.
It is given that, when $x < 0$ , $f(x) = 1 - x$ , so $x$ can take values like $x = - 1, - 2, - 3, - 4,...$ .
Let’s substitute the values of $x$ in the function.
For $x = - 1$ , $f( - 1) = 1 - ( - 1) = 1 + 1 = 2$ . So, the point is $( - 1,2)$ .
For $x = - 2$ , $f( - 2) = 1 - ( - 2) = 1 + 2 = 3$ . So, the point is $( - 2,3)$ .
For $x = - 3$ , $f( - 3) = 1 - ( - 3) = 1 + 3 = 4$ . So, the point is $( - 3,4)$ .
For $x = - 4$ , $f( - 4) = 1 - ( - 4) = 1 + 4 = 5$ . So, the point is $( - 4,5)$ .
We can keep on finding the point since there is no limit for the $x$ value, so we will stop here. Let us find the points for the next condition.
It is given that, when $x = 0$ , $f(x) = 1$ . Here $x$ has only one value that is 0, so $f(0) = 1$ . So, the point is $(0,1)$ .
Now let us find the points for the next condition.
It is given that, when $x > 0$ , $f(x) = x + 1$ , so $x$ can take values like $x = 1,2,3,4,...$ .
Let’s substitute the values of $x$ in the function.
For $x = 1$ , $f(1) = 1 + 1 = 2$ . So, the point is $(1,2)$ .
For $x = 2$ , $f(2) = 2 + 1 = 3$ . So, the point is $(2,3)$ .
For $x = 3$ , $f(3) = 3 + 1 = 4$ . So, the point is $(3,4)$ .
For $x = 4$ , $f(4) = 4 + 1 = 5$ . So, the point is $(4,5)$ .
Now let’s plot these points in the graph with the scale $x$ axis $1unit = 1cm$ and $y$ axis $1unit = 1cm$ and join the points.

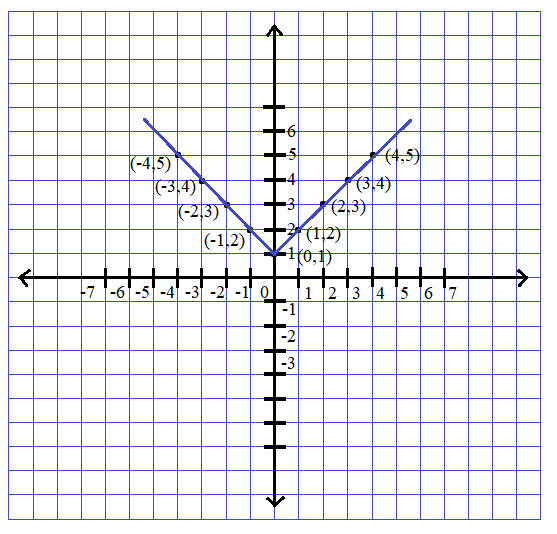
This is the required graph for the given function.

Note: Since the condition of the given problem doesn’t have any limit point, we have found some points to plot it in the graph. Point to remember while drawing graph: Scale of the graph is important; it has to be uniform. The given function doesn’t stop anywhere since $x$ has indefinite values, we will be getting a value of $y$ for each value of $x$ .