Question
Question: The function f defined by f(x) = \(f:\lbrack 1,\infty) \rightarrow \lbrack 1,\infty)\) is –...
The function f defined by f(x) = f:[1,∞)→[1,∞) is –
A
Every where continuous
B
Discontinuous at all integer values of x
C
Continuous at x = 0
D
None of these
Answer
Discontinuous at all integer values of x
Explanation
Solution
f(x) = 
 Q sin πx > 0
Q sin πx > 0
2nπ < πx < (2n +1) π
2n < x < 2n + 1, n ∈ I and if sin πx < 0
(2n + 1) < πx < (2n + 2)π
2n + 1 < x < 2n + 2, n ∈ I and sin πx = 0
if x = 0, 1, 2, …..
f(x)=⎩⎨⎧limt→∞1+(1+sinπx)t11−(1+sinπx)t1,2n<x<2n+1limt→∞(1+sinπx)t+1(1+sinπx)t−1,2n+1<x<2n+2
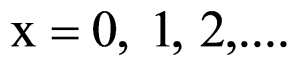
= 
k ∈ I, f(k) = 0, but  f(x) = 1 or – 1
f(x) = 1 or – 1
according as k ∈ (2n, 2n + 1) or k ∈ (2n + 1, 2n + 2)
