Question
Question: The function arctan(sinx + cosx) is increasing in the interval [a] \(\left( \dfrac{\pi }{4},\dfrac...
The function arctan(sinx + cosx) is increasing in the interval
[a] (4π,2π)
[b] (−2π,4π)
[c] (0,2π)
[d] (−2π,2π)
Solution
Hint: Use the fact that if f(x) is an increasing function, then f′(x)≥0. Alternatively, use the fact that if f(x) is an increasing function, then fog(x) is an increasing function whenever g(x) is increasing and fog(x) is a decreasing function whenever g(x) is a decreasing function.
Complete step-by-step solution -
We have f(x) = arctan(sinx+cosx)
Differentiating both sides, we get
f′(x)=dxd(arctan(sinx+cosx))
We know from chain rule of differentiation that dxd(f(g(x)))=d(g(x))df(g(x))dxd(g(x))
Hence f′(x)=d(sinx+cosx)darctan(sinx+cosx)dxd(sinx+cosx)
We know that dxdarctanx=1+x21
Hence we have
f′(x)=(sinx+cosx)2+11dxd(sinx+cosx)
We know that dxd(f(x)+g(x))=dxd(f(x))+dxd(g(x))
Using , we get
f′(x)=1+(sinx+cosx)21(dxdsinx+dxdcosx)
Since dxdsinx=cosx and dxdcosx=−sinx, we have
f′(x)=1+(sinx+cosx)21(cosx−sinx)
Now for f(x) to be increasing, we have
f′(x)≥0
Hence, we have
1+(sinx+cosx)21(cosx−sinx)≥0
Since 1+(sinx+cosx)21>0 , we have
(cosx−sinx)≥0
Hence cosx>sinx
In the interval (−2π,4π) cosx>sinx.
Hence we have
In the interval (−2π,4π) f(x) is increasing.
Hence option [b] is correct.
Note: Alternatively, we have,
arc tanx is an increasing function. Hence arctan(cosx+sinx) is increasing whenever sinx+cosx is increasing.
Now sinx +cosx =21(sin(x−4π))
Now we know that sinx is an increasing function in the interval (2−π,2π)
Hence sinx+cosx is increasing in the interval (2−π−4π,2π−4π)=(4−3π,4π)
Hence sinx + cosx is increasing in the interval (2−π,4π)
Hence option [b] is correct.
Graph of arctan(sinx+cosx)
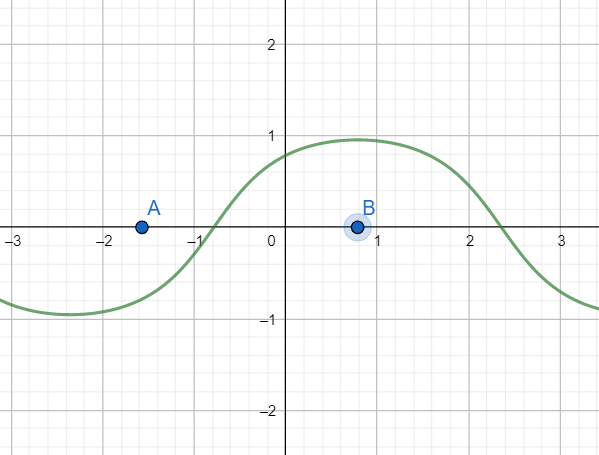
As is evident from the graph that f(x) is increasing in interval [A,B], where A=2−π and B=4π.
